Lista de Exercicios - UnB de Cálculo 1 da UnB - Lista 4

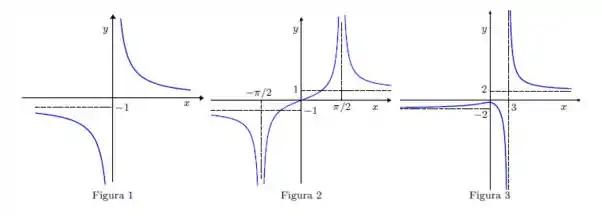
Explique o que significa dizer que a reta x = a é uma assíntota vertical da função . Em

seguida, considerando as funções esboçadas nos gráficos abaixo, determine as assíntotas verticais sugeridas por cada um deles.

No limite quando o numerador se aproxima de um número diferente de

zero e o denominador tende para zero com um sinal definido, temos um limite infinito. Neste caso, é necessário estudar o sinal da fração quando x está próximo de a, de modo a decidir se o limite é ou . Por exemplo, , pois o numerador se aproxima de e o denominador se aproxima de zero por valor negativos, pois x > 1 (lembre que o limite é pela direita). Assim, a fração tem sinal negativo e, em módulo, fica muito grande.

Siga este procedimento para calcular os limites abaixo.

No limite quando o numerador se aproxima de um número diferente de

zero e o denominador tende para zero com um sinal definido, temos um limite infinito. Neste caso, é necessário estudar o sinal da fração quando x está próximo de a, de modo a decidir se o limite é ou . Por exemplo, , pois o numerador se aproxima de e o denominador se aproxima de zero por valor negativos, pois x > 1 (lembre que o limite é pela direita). Assim, a fração tem sinal negativo e, em módulo, fica muito grande. Siga este procedimento para calcular os limites abaixo.

No limite quando o numerador se aproxima de um número diferente de

zero e o denominador tende para zero com um sinal definido, temos um limite infinito. Neste caso, é necessário estudar o sinal da fração quando x está próximo de a, de modo a decidir se o limite é ou . Por exemplo, , pois o numerador se aproxima de e o denominador se aproxima de zero por valor negativos, pois x > 1 (lembre que o limite é pela direita). Assim, a fração tem sinal negativo e, em módulo, fica muito grande. Siga este procedimento para calcular os limites abaixo.

No limite quando o numerador se aproxima de um número diferente de

zero e o denominador tende para zero com um sinal definido, temos um limite infinito. Neste caso, é necessário estudar o sinal da fração quando x está próximo de a, de modo a decidir se o limite é ou . Por exemplo, , pois o numerador se aproxima de e o denominador se aproxima de zero por valor negativos, pois x > 1 (lembre que o limite é pela direita). Assim, a fração tem sinal negativo e, em módulo, fica muito grande. Siga este procedimento para calcular os limites abaixo.

Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas

e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos

à assíntota para, em seguida, checar se cada um deles é de fato assíntota.

Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas

e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos

à assíntota para, em seguida, checar se cada um deles é de fato assíntota.

Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas

e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos

à assíntota para, em seguida, checar se cada um deles é de fato assíntota.

Explique o que significa dizer que a reta y = L é uma assíntota horizontal da função f.

Em seguida, considerando os gráficos esboçados no Exercício 1, determine as assíntotas

horizontais sugeridas por cada um deles.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Em alguns casos, o cálculo do limite no infinito de frações pode ser feito identificando se

os termos dominantes do numerador e do denominador, e colocando-se um deles em

evidência. Por exemplo,

Siga este procedimento para calcular os limites abaixo.

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Calcule os limites abaixo

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Determine todas as assíntotas das funções abaixo:

1. g(x) =

Seja , onde e são dados. Calcule os limites no infinito e, em seguida, use o Teorema do Valor Intermediário para mostrar que possui pelo menos uma raiz. O que se pode dizer se ?