UnB – Cálculo 1 – Lista de Exercícios 4 – Questão 1
Explique o que significa dizer que a reta x = a é uma assíntota vertical da função . Em
seguida, considerando as funções esboçadas nos gráficos abaixo, determine as assíntotas verticais sugeridas por cada um deles.
Passo 1
Fala galera, tudo bem? Dizer que uma função tem uma assíntota vertical significam duas coisas:
- Que existe um ponto do domínio no qual perto dele a função tende a um valor muuuuito grande (infinito)
- E no gráfico vemos que a função explode para mais ou menos infinito
E como encontramos esses pontos em uma função? Os candidatos são os pontos em que o denominador é zero! Isso porque quando o denominador se aproxima de zero, a divisão tem resultado cada vez maior
E em um gráfico? Vemos que a função “do nada” sobe muito ou desce muito
agora o problema nos deu 3 gráficos e pediu para identificarmos as assíntotas verticais, então agora que sabemos como identificar uma assíntota, vamos lá?
Vamos começar?
Passo 2
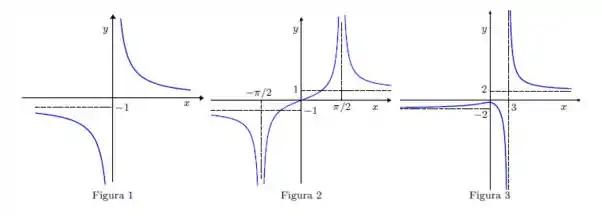
O primeiro gráfico que vamos analisar é esse aqui:
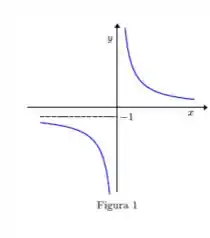
Vemos que a função vem vindo lá do lado esquerdo de e ao se aproximar do eixo , a função faz uma curva e vai lá pra baixo!
E atravessando o eixo , a função aparece lá bem de cima! Ou seja, ao se aproximar de , a função explode para
Assim como pela direita, mas agora explode para
E o que isso significa? ASSÍNTOTA VERTICAL!
E qual é a equação dessa assíntota?
Porque é perto desse ponto que a função explode!
Passo 3
Agora vamos analisar a figura 2:
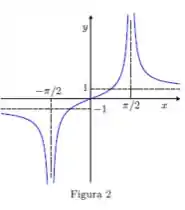
Olhando para essa figura vemos que a função explode em e também para .
Em ela explode para tanto pela direita quanto pela esquerda
Agora em ela explode para pelos dois lados
De qualquer forma, temos duas assíntotas verticais!
Beleza?
Passo 4
Agora vamos analisar a figura 3:
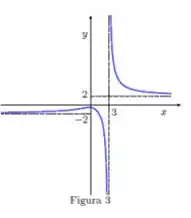
Já nessa última figura vemos que a função vai para quando pela esquerda. E pela direita a função explode para .
Então aqui temos mais outra assíntota vertical
E é isso! Espero ter ajudado!