Provas de Física 1 - UERJ de Física I da UERJ - Primeira Prova
Uma corrente com quatro elos ( cada) é puxada para cima por uma força vertical (assinalada na figura abaixo) de módulo igual a .

Desenhe um diagrama das forças que atuam sobre cada elo.
Escolha um sistema de referência e escreva as forças nesse referencial.
Escreva as leis de Newton para o problema e deduza as equações pertinentes.
Calcule a aceleração da corrente.
Calcule as forças que atuam nos elos.
Ver solução completaUm pintor de está sobre uma plataforma de suspensa por uma roldana ideal (veja a figura abaixo). Puxando a corda ele faz a plataforma subir com aceleração de .
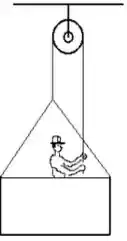
Desenhe o diagrama de forças que atuam no pintor e na plataforma e escolha um sistema de referência.
Escreva as leis de Newton para o pintor e para a plataforma.
Determine cada uma das forças que atuam no pintor.
Determine cada uma das forças que atuam na plataforma.
Ver solução completaUma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
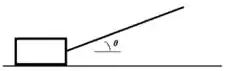
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
a) Escolha um referencial e desenhe um diagrama das forças que atuam sobre o caixote.
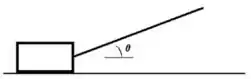
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
b) Calcule a força que o solo exerce no caixote.
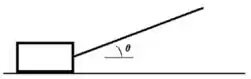
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
d) Calcule o trabalho realizado por cada uma das forças em um deslocamento do caixote de D metros
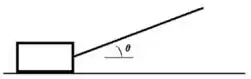
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
e) Qual seria a aceleração do caixote se o coeficiente de atrito baixasse, repentinamente, para a metade do seu valor?
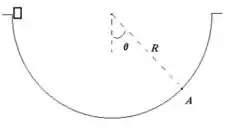
4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
a) Qual o módulo da velocidade do cubo de gelo quando ele passa pelo fundo da vasilha?
4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
b) Faça um diagrama das forças que atuam no cubo de gelo quando ele passa pelo fundo da vasilha
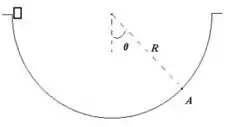
4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
c) Qual a força que a vasilha exerce sobre o cubo de gelo quando este passa pelo fundo da vasilha?

4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
d) Qual o módulo da velocidade do cubo de gelo no ponto assinalado na figura?

4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
e) Qual a força que a vasilha exerce sobre o cubo de gelo quando este passa ponto assinalado na figura.

Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
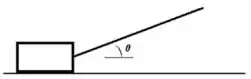
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
a) Escolha um referencial e desenhe um diagrama das forças que atuam sobre o bloco.
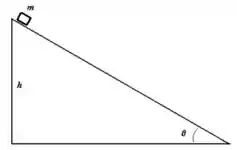
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
b) Calcule as forças que atuam no bloco.
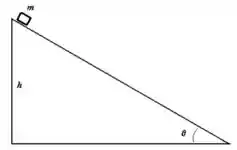
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
c) Calcule a aceleração do bloco.
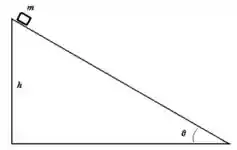
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
d) Calcule o trabalho de cada uma das forças que atua sobre o bloco do início ao fim da rampa.
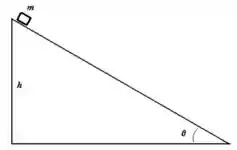
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
e) Calcule a energia mecânica do bloco no fim da rampa.
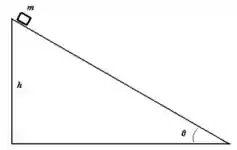
8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
Ver solução completa8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completa8. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completaUma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
Ver solução completa10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completa10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completa10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
d)
Ver solução completa10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
e)
Ver solução completa10. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
f)
Ver solução completaUma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
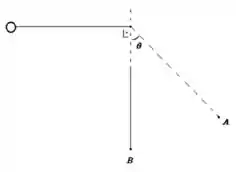
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
a) Qual deve ser o módulo da velocidade da bolinha no ponto mais baixo?
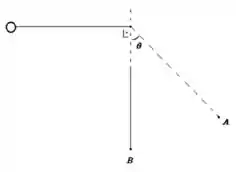
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
b) O módulo da força que o fio faz na bolinha no ponto mais baixo?
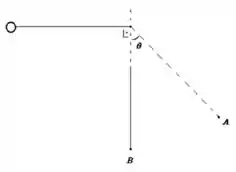
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
c) O módulo da velocidade da bolinha no ponto .
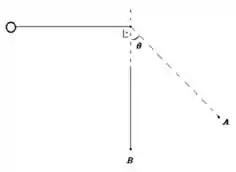
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
d) O módulo da força que o fio faz na bolinha no ponto .
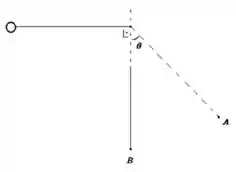
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
e) Qual deveria ser o módulo da velocidade mínima da bolinha no ponto inicial para que a bolinha desse a volta completa?
13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
a)
Ver solução completa13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
b)
Ver solução completa13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
c)
Ver solução completa13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
d)
Ver solução completa13. Considere um objeto sujeito a uma força dada por . Calcule o trabalho dessa força do ponto até o ponto nos seguintes caminhos:
e)
Ver solução completaUma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
c) Calcule o coeficiente de atrito entre o solo e o caixote.
16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .

a) Desenhe um diagrama das forças que atuam em cada um dos blocos e as escreva em um referencial determinado por você
Ver solução completa16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .

b) Determine a aceleração do conjunto e as forças que atuam em cada bloco.
Ver solução completa16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .

c) Se a posição dos blocos fosse trocada o que mudaria nas forças e na aceleração?
Ver solução completa16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .

d) Calcule o trabalho das forças em um arraste de
Ver solução completa16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .

e) Se os blocos se encontravam em repouso, calcule a energia cinética dos blocos após o arraste de .
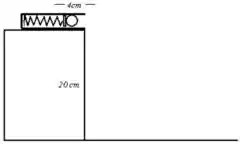
Ver solução completa17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
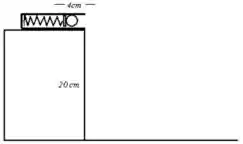
a) Qual a energia mecânica inicial da bolinha?
Ver solução completa17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
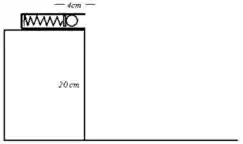
b) Qual a velocidade da bolinha quando ela chega à boca do canhão?
Ver solução completa17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
c) O tempo que a bolinha leva para alcançar o solo.
Ver solução completa17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
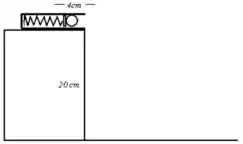
d) A velocidade da bolinha no instante imediatamente anterior ao choque com o solo.
Ver solução completa17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
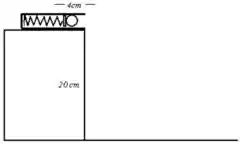
e) O ponto em que a bolinha toca o solo (sua posição quando chega no chão).
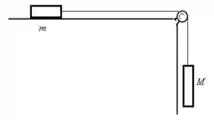
Ver solução completa18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
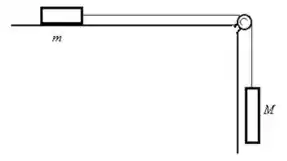
a) Faça um diagrama das forças que atuam sobre os blocos, escolha um referencial e escreva as forças nesse referencial.
Ver solução completa18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
b) Calcule as forças que atuam nos blocos.
Ver solução completa18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
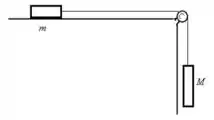
c) Calcule a aceleração dos blocos.
Ver solução completa18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
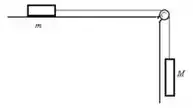
d) Calcule o trabalho dessas forças em um deslocamento de .
Ver solução completa18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
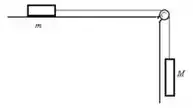
e) Considerando que na situação inicial os blocos estão em repouso, qual seria a variação de energia cinética do sistema em um deslocamento de ?
Ver solução completa