UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 18d
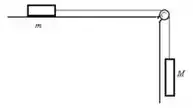
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
d) Calcule o trabalho dessas forças em um deslocamento de .
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema temos um bloco de massa sob uma superfície que está ligado a uma corda que passa por uma polia sem atrito onde na outra extremidade da corda há um bloco de massa suspenso.
Sabendo que o coeficiente de atrito entre o primeiro bloco e a superfície é de , queremos obter o trabalho que cada força realiza ao sistema se mover por .
Parece complicado? 🤔
Para calcular o trabalho de uma força, temos
Onde é o ângulo entre a força e o deslocamento.
Vamos analisar cada bloco e as forças que atuam para determinar o trabalho de cada uma.
Bora lá! 😬
Passo 2
Começando pelo bloco
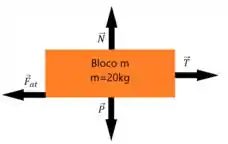
Perceba que as forças que atuam na vertical, no caso e , saó perpendiculares o movimento, portanto, , ou seja
Já a força de atrito foi calculada anteriormente como
Como a força de atrito aponta no sentido contrário ao movimento, o ângulo , ou seja,
Por fim, a força tração no bloco que vamos chamar de para diferenciar foi calculada anteriormente como
Como ela aponta na direção do movimento,
Bacana, não é? 😬
Passo 3
Agora vamos fazer a mesma análise no bloco
Como nesse bloco o movimento é vertical, o trabalho será na vertical.
O bloco se move para baixo, então o ângulo que o força faz com o movimento é , logo
Por último, a força peso do bloco aponta na direção do movimento, logo
Pegou o esquema? Responde Aí! 😁
