UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 12a
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
a) Qual deve ser o módulo da velocidade da bolinha no ponto mais baixo?
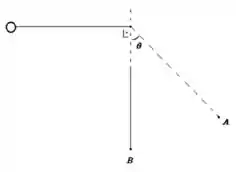
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nessa questão temos uma bolinha de massa que está amarrada por uma corda de comprimento e é solta com velocidade inicial .
Com isso queremos saber qual é a velocidade máxima que a bolinha atinge ao passar pelo ponto mais baixo da trajetória.
E aí, como fazemos isso? 😐
Nesse caso, podemos usar a lei de conservação de energia para descobrir a energia mecânica da bolinha no momento em que ela é solta.
Nesse instante a bolinha possui apenas energia potencial já que a velocidade é , já no momento mais baixo do trajeto, toda a energia potencial foi convertida em energia cinética.
A partir daí podemos começar nosso problema. Bora lá 😉
Passo 2
Inicialmente, a bolinho possui apenas energia potencial gravitacional, ou seja
Onde no caso, é o comprimento da corda
Já no ponto mais baixo, toda energia inicial foi convertida em energia cinética dada por
Como e são iguais, podemos igualar essas duas equações
Portanto a velocidade máxima da bolinha é dada por
Sacou como faz? Responde Aí! 😉
