UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 18c
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
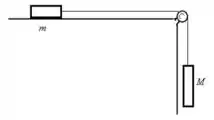
c) Calcule a aceleração dos blocos.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos um bloco de massa sob uma superfície que está ligado a uma corda que passa por uma polia sem atrito onde na outra extremidade da corda há um bloco de massa suspenso.
Sabendo que o coeficiente de atrito entre o primeiro bloco e a superfície é de , queremos obter a aceleração dos blocos.
Parece complicado? 🤔
Para resolver esse problema temos que aplicar a segunda lei de Newton que diz que a força resultante é igual a massa multiplicada pela aceleração
No caso, é o somatório das forças que contribuem para o movimento, ou seja, o somatório das forças que agem na direção do movimento.
Já da fórmula de é a soma das massas do sistema, ou seja,
Sacou? Bora começar! 😁
Passo 2
Analisando as forças que atuam no sistema, vemos que as forças peso da massa e a normal da massa não contribuem diretamente para o movimento.
Assim, somando as forças que atuam na horizontam em e as forças em , temos
Consideramos pois eles apontam em sentidos opostos, então devem se cancelar
Se e , então
Como a força é igual a massa vezes a aceleração, então
O que achou? Foi de boa? Responde aí! 😊
