UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 17b
17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:
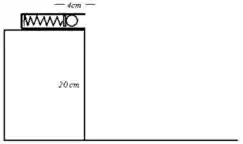
b) Qual a velocidade da bolinha quando ela chega à boca do canhão?
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema temos uma bolinha de massa que é colocada em um canhão de mola localizada a uma altura cuja constante elástica da mola é e é comprimida por antes de ser solta.
Com isso, queremos saber qual é a velocidade da bolinha quando ela é solta e passa pela boca do canhão.
E agora? como fazemos isso? 🤔
Para resolver esse problema podemos aplicar a lei de conservação de energia já que não há perdas no sistema do momento em que a bola é solta até o momento em que ela passa pela boca do canhão.
Pela lei de conservação de energia a energia mecânica inicial é igual a energia mecânica final.
Parece tranquilo? 😁
Passo 2
No momento inicial a bolinha está parada, está comprimindo a mola e está a uma altura do solo.
No momento final a bolinha está em movimento, portanto possui uma velocidade e consequentemente energia cinética, porém a bolinha não comprime mais a mola, logo, não possui energia potencial elástica.
Escrevendo as equações das energias do sistema, temos
No instante final e inicial as energias potenciais gravitacionais são iguais já que possuem a mesma altura .
Portanto podemos cancelá-las...
Bacana, não é? 😊
Passo 3
A energia potencial elástica é calculada como
Já a energia cinética é calculada como
Como vimos que , então
Isolando
Como , e
Pegou o esquema? Responde Aí! 😁
