UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 7d
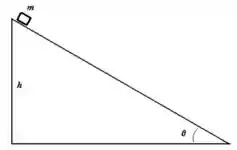
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
d) Calcule o trabalho de cada uma das forças que atua sobre o bloco do início ao fim da rampa.
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos um bloco de massa que está sob uma superfície inclinada que faz um ângulo com a horizontal e tem altura . Além disso a superfície e o bloco possuem atrito cujo coeficiente de atrito é dado por .
Com essa disposição queremos obter o trabalho de cada força quando o bloco se move do topo da rampa até a base.
Parece de boa, não é? 😉
Sabemos que o trabalho de uma força é dado pelo produto dela com a distância percorrida no seu sentido é são calculadas por
Isso significa que forças perpendiculares ao movimento não realizam trabalho.
Vamos analisar as forças do nosso sistema a partir do deslocamento. 😁
Passo 2
As forças são dadas por
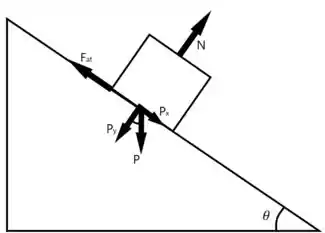
Com isso já podemos cravar que e não realizam trabalho já que são forças perpendiculares ao movimento.
Para a força , apenas sua componente realiza trabalho, ou seja
Como obtemos anteriormente que , temos
Tranquilo até aqui? 😎
Passo 3
Para a força de atrito, como ela aponta para o lado contrário do deslocamento, o trabalho será negativo...
Anteriormente calculamos que , portanto
Mas o que é ?
Temos que a rampa forma um triangulo retângulo, então pela lei dos senos temos
Portanto, os trabalhos são dados por
É isso! Essa resolução te ajudou? Responde Aí! ✌
