UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 7e
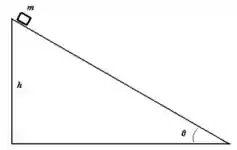
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
e) Calcule a energia mecânica do bloco no fim da rampa.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos um bloco de massa que está sob uma superfície inclinada que faz um ângulo com a horizontal e tem altura . Além disso a superfície e o bloco possuem atrito cujo coeficiente de atrito é dado por .
Nessa situação, queremos descobrir qual é a energia mecânica do bloco ao chegar na base da rampa.
E agora, o que temos que fazer? 🤔
Nesse caso podemos aplicar a lei da conservação de energia com uma pequena diferença, nesse sistema há atrito do bloco com a superfície então a maneira de se obter a energia mecânica no fim é um pouco diferente.
E aí, entendeu essa parte? 😉
Passo 2
Podemos dizer que a energia final do sistema é igual a energia inicial do sistema menos as perdas que ocorreram no caminho, perdas essas que foram feitas pela força de atrito.
Inicialmente a energia é dada pela força potencial gravitacional, ou seja
Já na base da rampa, não há mais energia potencial, mas há energia cinética, ou seja
Já as perdas de uma força s��o dadas pelo trabalho realizado no deslocamento.
Anteriormente vemos que o trabalho realizado pela força de atrito em modulo é dada por
Portanto, podemos dizer que a energia mecânica final é dada por
Substituindo e , temos
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
