UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 12e
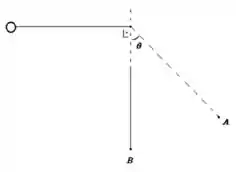
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
e) Qual deveria ser o módulo da velocidade mínima da bolinha no ponto inicial para que a bolinha desse a volta completa?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão temos uma bolinha de massa que está amarrada por uma corda de comprimento e é solta com velocidade inicial .
Com isso queremos saber qual deve ser a velocidade mínima de para que a bolinha dê a volta completa.
E aí, como fazemos isso? 😐
Para responder essa pergunta, podemos aplicar a lei da conservação de energia que diz que a energia de um sistema não é dissipada, mas sim transformada, ou seja, a energia inicial é igual a energia final.
Então inicialmente, a bolinha deve ter energia suficiente para alcançar o ponto mais alto da trajetória.
Sacou o que temos que fazer? Bora lá! 😉
Passo 2
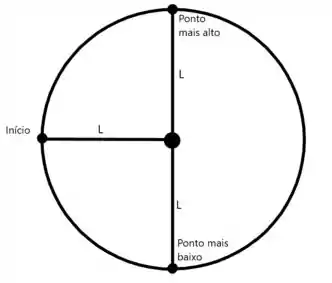
Vamos começar pelo fim. Qual é a energia potencial que a bolinha possui no ponto mais alto do trajeto?
A energia potencial é calculada como
No caso, e são constantes em todo o trajeto, mas corresponde a altura mais alta que é possível, ou seja, duas vezes o comprimento
Tranquilo até aqui? 👀
Passo 3
Portanto energia contida no sistema deve ser maior que
Com isso, no ponto inicial, a energia potencial é dada com e a energia cinética como
Igualando a energia inicial com a energia final, vamos obter
Simplificando e isolando em um lado...
Portando para dar uma volta completa
Fim! Iae, o que achou? Responde Aí! 😁
