17. Uma bolinha de massa é colocada no canhão-de-mola como mostra a figura (abaixo à esquerda). Sabendo que a constante elástica da mola é e que sua compressão é de , responda:

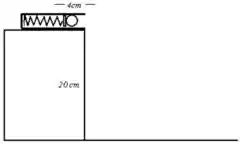
e) O ponto em que a bolinha toca o solo (sua posição quando chega no chão).

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema temos uma bolinha de massa que é colocada em um canhão de mola localizada a uma altura cuja constante elástica da mola é e é comprimida por antes de ser solta.

Com isso, queremos saber qual é a posição horizontal que a bolinha toca o solo ao cair, ou seja, a distância horizontal que a bolinha percorreu.

E agora? como fazemos isso? 🤔

Após a bolinha ser arremessada pelo canhão nosso problema se transforma em um problema de lançamento obliquo.

Nesses casos, a velocidade horizontal do projetil (no nosso caso, a bolinha) é constante e a velocidade vertical é acelerada devido a ação de aceleração gravitacional.

Anteriormente calculamos a velocidade horizontal da bolinha na saída do canhão como

E também calculamos o tempo que a bolinha demora a tocar o solo como

Com essas informações somos capazes de encontrar o ponto de impacto.

Tranquilo até aqui? 😬