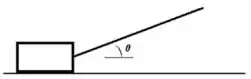
3. Um caixote de massa é puxado por meio de uma corda (como mostra a figura abaixo à esquerda) com uma velocidade constante. A tração na corda é e o ângulo entre a corda e a horizontal é .
c) Calcule o coeficiente de atrito entre o solo e o caixote.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema temos uma caixa com massa que é puxado por uma corda que faz um ângulo com a horizontal e que possui uma tração na corda. Nessa situação, queremos obter o coeficiente de atrito entre o solo e o caixote.
E aí, como fazemos isso? 👀
Primeiramente, sabemos que a força de atrito é dada por
E como o problema já disse que o caixote se move a uma velocidade constante, podemos afirmar que as forças que agem sobre ele estão em equilíbrio.
Assim como podemos determinar ? 🤔
Passo 2
Agora vamos analisar as forças verticais que agem sobre o caixote...
Como o sistema está em equilíbrio, as forças horizontais se anulam.
Horizontalmente sabemos que a força de atrito age sobre o caixote e também a componente horizontal da tração.

Dessa forma, podemos perceber que a força é igual a forca
Pela lei dos cossenos, sabemos que
Como , então
Como no item anterior vemos que , vamos obter que o coeficiente de atrito é dado por
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
