UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 12d
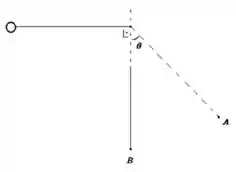
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
d) O módulo da força que o fio faz na bolinha no ponto .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos uma bolinha de massa que está amarrada por uma corda de comprimento e é solta com velocidade inicial .
Com isso queremos saber qual é a força que o fio faz na bolinha ao passar pelo ponto .
E aí, como fazemos isso? 😐
As únicas forças que atuam nesse sistema são a força peso e a força tração .
Queremos saber qual é a tração da corda no ponto . Pra isso, vamos desenhar as forças que atuam na bolinha quando ela está no ponto e ver o que podemos encontrar.
Bora lá! 😎
Passo 2
A força peso sempre aponta para baixo, já a tração aponta na direção do eixo de rotação, ou seja
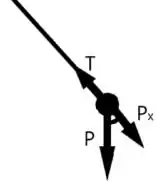
Para obter , podemos decompor em duas partes, sendo a parte a parte que nos interessa.
Por semelhança de triângulos, o ângulo entre e é então pela lei dos cossenos, temos
E como ...
Sabemos que , portanto...
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
