UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 18e
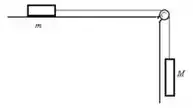
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
e) Considerando que na situação inicial os blocos estão em repouso, qual seria a variação de energia cinética do sistema em um deslocamento de ?
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos um bloco de massa sob uma superfície que está ligado a uma corda que passa por uma polia sem atrito onde na outra extremidade da corda há um bloco de massa suspenso.
Sabendo que o coeficiente de atrito entre o primeiro bloco e a superfície é de , queremos obter a variação da energia cinética do sistema ao se mover por .
Parece complicado? 🤔
A energia cinética de um sistema é dada por
No caso, temos que encontrar a velocidade após o sistema se mover por e a massa da fórmula é a massa do sistema, ou seja,
Tranquilo até aqui? 😉
Passo 2
Anteriormente calculamos a aceleração do sistema como
A partir da equação de Torricelli, podemos obter a velocidade final dos blocos como
Como o sistema parte do repouso,
Substituindo e , temos
Tirando a raiz...
Bacana, não é? 😊
Passo 3
Substituindo esse valor de na fórmula da energia cinética, temos
Com , e
Sacou como faz? Responde Aí! 😉
