Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Simples

Ver Teoria
Exercício 712345689101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263

Enunciado

Um pintor de 80   kg está sobre uma plataforma de 40   kg suspensa por uma roldana ideal (veja a figura abaixo). Puxando a corda ele faz a plataforma subir com aceleração de 1 2   m/ s 2 .

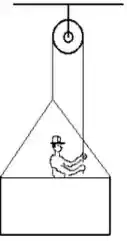
a ) Desenhe o diagrama de forças que atuam no pintor e na plataforma e escolha um sistema de referência.

b ) Escreva as leis de Newton para o pintor e para a plataforma.

c ) Determine cada uma das forças que atuam no pintor.

d ) Determine cada uma das forças que atuam na plataforma.

Passo 1

a )

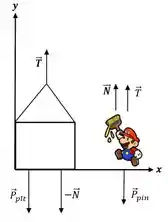
Além das forças que já estamos acostumados a colocar em nossos corpos, é importante percebermos que existe uma normal sobre o pintor porque ele está em contato com a plataforma e por causa da Terceira Lei de Newton vai existir, sobre a plataforma, a reação dessa normal apontando no sentido oposto.

Passo 2

b ) Vamos montar as equações do movimento usando a Segunda Lei de Newton para cada um dos corpos e vamos adotar para cima como sentido positivo.

Para a plataforma

F r → = m p l t . a → = T → + P → p l t + N →

T - m p l t . g - N =   m p l t . a

E para o pintor

F r → = m p i n . a → = T → + P → p i n + N →

T - m p i n . g + N = m p i n . a

Passo 3

c ) O peso do pintor é dado por

P p i n = m p i n g = 80 × 9,8

P p i n = 784 N

Para achar a tração podemos somar as duas equações do passo 2 no sistema:

T - m p l t . g - N =   m p l t . a T - m p i n . g + N = m p i n . a

2 T - m p l t . g - m p i n . g =   m p l t . a + m p i n . a

Isolando T :

T = a + g m p i n + m p l t 2 = 0,5 + 9,8 80 + 40 2

T = 618 N

Voltando ao sistema e olhando para a segunda equação do passo 2:

T + N - m p i n . g =   m p i n . a

Isolando N :

N = m p i n a + g - T = 80 0,5 + 9,8 - 618

N = 206 N

Passo 4

d ) Já calculamos a normal e a tração no passo anterior, e sabemos que ambas as forças são reações às forças do pintor. Agora só falta o peso da plataforma, assim:

P p l t = m p l t g = 40 × 9,8

P p l t = 392 N

Resposta

a )

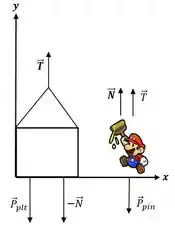
b ) Para a plataforma

T - P p l t - N =   m p l t . a

E para o pintor

T + N - P p i n = m p i n . a

c ) T = 618 N , P p i n = 784 N e N = 206 N

d )   T = 618 N , P p l t = 392 N e N = 206 N

Exercícios de Livros Relacionados

Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas m a = 30,0k g , m b = 40,0k g , m c = 10,0k g . Quando o con
Ignorando qualquer forma de atrito no sistema mostrado na Figura 5.16. A) encontre a relação entre as massas m e M para que o sistema fique em equilíbrio; B) calcule a aceleração dos blocos se M = 2 m
Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in
Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo
Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es