Uma barra homogênea de massa e comprimento é presa por uma de suas extremidades e posta para oscilar como um pêndulo físico sob ação da gravidade . Sabendo que o momento de inércia da barra em relação à sua extremidade é , resolva os itens a seguir:
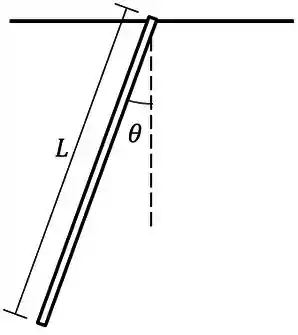
- Deduza a equação de movimento para arbitrário e diga qual a condição (se houver) para o movimento harmônico. Neste caso, qual será a frequência das oscilações?
- Resolva a equação do oscilador harmônico sabendo que o pendulo é inicialmente solto do repouso com ângulo igual a em relação à posição de equilíbrio.
- Adimita agora que haja um torque dissipativo que seja proporcional à velocidade angular, isto é, , onde é uma constante positiva. Escreva a nova equação de movimento e deduza qual deve ser a condição satisfeita por para que haja amortecimento subcritico. Não é necessário resolver esta nova equação de movimento.
Passo 1
a)
Temos aqui um pendulo físico, a forma de resolver é igual ao exemplo da teoria. Sabemos que para rotação
No caso da barra
Vamos calcular o torque em relação ao centro de rotação, a única força que faz torque é o peso. O torque do peso vai ser
Nesse caso
Passo 2
Como , vamos ter
Para pequenos valores de :
Então:
Pronto! Já está no formato da equação do MHS.
Então ótimo. Comparando com a equação do MHS, temos que:
Passo 3
Ele quer a frequência então
Passo 4
b)
Se ele é solto do repouso e a o ângulo inicial é , vamos ter
Vamos resolver a EDO, primeiro achando a equação auxiliar
Esse é o caso de raízes complexas, com a parte real sendo zero
Vamos ter então
Vamos para as condições iniciais agora
Então
Então
Dessa forma temos a equação de
Passo 5
c)
Vamos ter agora um torque extra, então a EDO fica
Lembrando que
Para termos um amortecimento subcrítico devemos ter da equação auxiliar menor que zero.
A equação auxiliar é
Então
Dessa forma
Normalmente teríamos
Como vamos ter na verdade