Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulo Físico

Ver Teoria
Exercício 21123456789101112131415161718192022232425262728293031323334

Enunciado

PUCRIO – FIS1041 – G1 – 2019.2

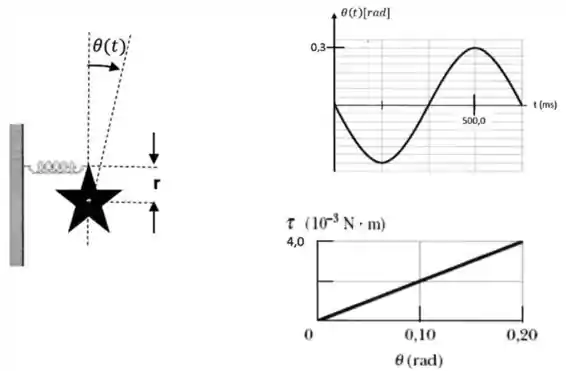
A figura mostra um objeto com forma de estrela, livre para girar ao redor de seu centro de massa e com a ponta superior presa a uma mola. O primeiro gráfico mostra a função θ t = θ M cos ⁡ ω t + φ [rad, ms] que descreve a posição angular θ da ponta superior da estrela em função do tempo t . O segundo gráfico mostra o torque τ produzido pela força elástica da mola em função de θ . A relação entre a deformação x do comprimenrto da mola e o ângulo θ é dada por x t = r θ t . A relação entre o torque aplicado à estrela e a força exercida pela mola é dada, para pequenos ângulos, por τ = r F . Considere r = 0,25   m .

Determine:

(a) a constante elástica k da mola.

(b) a frequência angular ω 0 do MHS resultante.

(c) o momento de inércia I da estrela

(d) a constante de fase φ .

Passo 1

(a) Tome que a força elástica é dada por

| F e | = k ⋅ Δ x

Na qual Δ x é a diferença entre a posição da ponta da estrela é até a posição de equilíbrio do sistema massa mola. No nosso caso podemos reescrever nossa equação como

F e = k ⋅ r ⋅ Δ θ

Na qual, podemos fazer Δ x = r ⋅ Δ θ para pequenas variações de Δ θ . Como não não possuímos um gráfico de força, devemos usar o de torque mesmo hahaha.

Tome que o torque é dado por

τ → = r → × F → → | τ | = r | F |

Visto F → e r → são perpendiculares. Assim temos que

F e = τ r

E consequentemente

τ = k ⋅ r 2 ⋅ Δ θ

Assim temos que

k = τ r 2 ⋅ Δ θ

Olhando pro segundo gráfico temos um relação linear entre Δ θ e τ , assim tome que θ = 0,1 → τ = 2,0 × 10 - 3   N ⋅ m .

Logo

k = 2,0 × 10 - 3   N ⋅ m 0,25   m 2 ⋅ ( 0,1 ) = 3,2 × 10 - 1   N / m

Passo 2

(b) Bom, a frequência angular pode ser descrita como

ω 0 = 2 π T

Na qual T é o período. Olhando para nosso primeiro gráfico, temos que

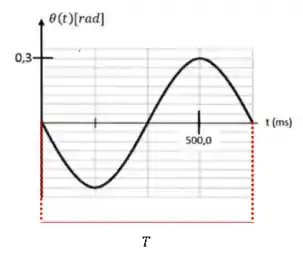
Ou seja,

T = 500   m s + 500 3 m s = 667   m s = 0,667   s  

Assim temos que

ω 0 = 2 π 0,667   s = 9,42   r a d / s

Passo 3

(c) Vamos conversar um pouquinho ...

Visualize que, quando nossa mola ta se esticando, nossa estrela tente a manter seu centro de massa parado. Isso é explicado pela primeira lei de newton, inércia. Logo implica que a mola irá tender a girar a partir do seu centro de massa. Assim teremos uma relação entre a energia potencial da mola e a energia de rotação da estrela dada por

1 2 k ⋅ Δ x 2 = 1 2 I ω 2

Na qual, nosso ω referece a estela especificamente.

Lembre que por definição

ω = d θ d t

Novamente, perceba, estamos trabalhando com ângulos pequenos. Além disso, nosso problema se refere à um oscilador, logo

d θ d t = ω 0 θ t

Além disso,

Δ x = r   Δ θ

Repare que o nosso gráfico tomando θ 0 = 0 ⟹ θ ( t ) ≡ Δ θ

Assim temos

k ⋅ r 2 ⋅ Δ θ 2 = I ⋅ ω 0 2 ⋅ Δ θ 2

Ou seja

I = k ⋅ r 2 ω 0 2 = 0,32 N m 0,25   m 2 9,42 r a d s 2 ≈ 2,25 × 10 - 4   k g ⋅ m 2

Passo 4

(d) Bom, talvez esse seja nosso item mais tranquilo, visto que precisamos apenas analisar nossa função

θ t = θ M cos ⁡ ( ω t + φ )

Na qual θ M é nossa amplitude máxima, ou seja, θ M = 0,3 .

Tome t = 0 , então

θ 0 = 0 = cos ⁡ φ → φ = 2 n + 1 π 2

Resumindo nosso arco trigonimétrico entre 0 e 2 π , ficamos com solução dada em

φ = π 2

ou

φ = 3 π 2

Resposta

  1. k = 3,2 × 10 - 1   N / m
  2. ω 0 = 9,42   r a d / s
  3. I = 2,25 × 10 - 4   k g ⋅ m 2
  4. φ = π / 2 ou φ = 3 π / 2

Exercícios de Livros Relacionados

No exemplo que envolve a Fig. 15-11, vimos que um pêndulo físico em forma de régua possui um centro de oscilação a uma distância 2L/3 do ponto de suspensão. Mostre que a distância entre o ponto de sus
Na Fig. 15-40, o pêndulo é formado por um disco uniforme de raio r = 10,0 c m e 500 g de massa preso a uma barra homogênea de comprimento L = 500 m m e 270 g de massa. (a) Calcule o momento de inércia
Na Fig. 15-47a, uma placa de metal está montada em um eixo que passa pelo seu centro de massa. Uma mola com k = 2000 N / m está ligada a uma parede e a um ponto da borda da placa a uma distância, r =
Um pêndulo é formado suspendendo-se por um ponto uma barra longa e fina. Em uma série de experimentos o período é medido em função da distância x entre o ponto de suspensão e o centro da barra. (a) Se
Na Fig. 15-42, um pêndulo físico é formado por um disco uniforme (de raio R = 2,35 c m ) sustentado em um plano vertical por um pino situado a uma distância d = 1,75 c m do centro do disco. O disco é