Uma esfera homogênea com 0,5 kg de massa está livre para girar em torno de um eixo vertical que passa pelo seu centro. Uma mola de constante elástica k = N/m é ligada horizontalmente entre a borda da esfera no plano do equador e uma parede fixa. A figura ao lado mostra a vista de topo da esfera e da mola na sua posição de equilíbrio. Determine o período das pequenas oscilações que acontecem quando a esfera é levemente girada no plano do equador e em seguida liberada. Dado:
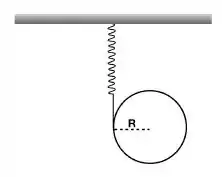
Passo 1
Vamos considerar o sentido anti-horário como o positivo. Ok? E vemos que a força elástica tá causando um torque no sentido horário, portanto negativo.
O torque causado pela força elástica vai ser então:
A força elástica vai ser:
Em que , para pequenas rotações, e é igual ao deslocamento angular a partir da posição de equilíbrio. Então:
Belezinha!
Passo 2
Vamos aplicar a segunda lei de Newton para rotações. Parece difícil, mas não é! Vai ficar assim:
Trocando I por :
Passo 3
Comparando com a equação do MHS:
Vemos que:
O período vai ser:
Substituindo os valores dados:
Resposta