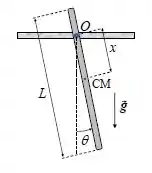
A figura ao lado mostra um pêndulo físico composto por uma barra uniforme de comprimento que pode oscilar livremente em torno de um eixo pelo ponto a uma distância do centro da barra.
- Considere e No instante a barra é abandonada a partir do repouso em um ângulo arbitrariamente pequeno com a vertical. Em segundos, a barra passa pela posição vertical pela primeira vez. Determine o valor de .
- Suponha agora que . Determine, em centímetros, o valor de que minimiza o período.
(Dados:
Passo 1
Neste caso temos uma barra de massa e momento de inércia , preso a um eixo em um ponto.
O primeiro passo é entender o diagrama de corpos livres e forças atenuantes:
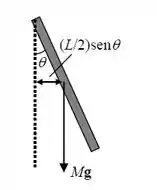
A equação de MHS pode ser descrita como:
(EQ 1)
Rearranjando os termos, temos que:
Como o ângulo é muito pequeno, podemos considerar então
(EQ 2)
Mas , logo:
Onde,
. (EQ 3)
Colocando o termo do momento de inércia em evidência, chegamos a:
(EQ 4)
Agora que já a expressão para o momento de inércia podemos substituir a EQ 4 na EQ 2.
No instante corresponde a 1/4 do período, assim:
Logo
Passo 2
Para minimizarmos o período temos que:
(EQ 5)
O período é descrito como:
(EQ 6)
Substituindo a EQ 6 na EQ 5, temos:
Então:
Substituindo os valores de e , chegamos à:
Resposta
a) 20
b) 3 cm