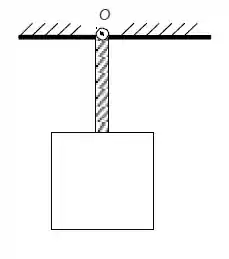
O pêndulo da figura abaixo é formado por uma haste de comprimento e uma chapa quadrada também de lado , presos no ponto de maneira que o conjunto possa se movimentar. Tanto a haste quanto a chapa são uniformes e possuem massa . Os momentos de inércia em torno dos centros de massa de uma haste e de uma chapa quadrada são, respectivamente, e .
- Calcule a distância entre o ponto e o centro de massa desse conjunto .
- Se o pêndulo é posto para oscilar em torno do ponto com ângulo pequeno, qual será o período de oscilação?
Passo 1
Vamos primeiro achar o centro de massa de cada peça. O centro de massa das peças fica no centro das peças, já que ambas são homogêneas. Então, em relação ao ponto O, os centros de massas são:
O centro de massa dois tem esse valor pois é essa a distância do ponto O até o centro da placa quadrada.
Pronto! Agora pra gente achar o centro de massa total a gente usa:
Essa é a distância procurada!
Passo 2
b)
Nesse item, a gente vai precisar primeiro achar o momento de inércia total de toda a peça em relação ao ponto O.
Esse momento vai ser dado por:
Onde é o momento do centro de massa resultante das duas peças e é a distância do centro de massa da peça em relação ao ponto O, ou seja, o resultado de
O complicado aqui é achar . Mas vamos pensar em como podemos fazer isso:
O centro de massa está na distância do ponto O. As peças que o cercam são a barra e o quadrado.
Podemos, então, calcular o momento de inercia de cada peça em relação ao centro de massa! Isso quer dizer: Calcular, usando o teorema dos eixos paralelos, o momento das peças em relação à
Para a barra:
Já que a distância do centro de massa da barra ao centro de massa é
E o momento do quadrado é:
Logo:
E:
Passo 3
Agora vamos calcular o período! De acordo com a nossa teoria, o cálculo da EDO do pêndulo físico é:
Como
Para pequenos valores de :
Então:
Onde , no nosso caso. E . Logo:
Resposta
a)
b)