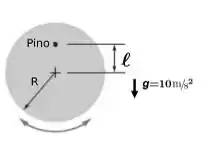
Conforme figura ao lado, um pêndulo é formado por um disco uniforme de massa M sustentado em um plano vertical por um pino situado a uma distância = 3m do centro de massa do disco. O raio do disco é R = 4 m. O pêndulo oscila com uma amplitude angular pequena. Dado que o momento de inércia de um disco homogêneo em relação ao seu centro de massa é , diga qual é a frequência angular de oscilação em rad/s.
a)
b)
c) 2
d)
e)
f)
g)
h)
Passo 1
Aqui nós vamos ter que aplicar a segunda lei de Newton para rotações!
E o torque resultante vai ser devido ao peso do disco, aplicado a uma distância do centro de rotação:
Para pequenas inclinações, . Então:
Trocando os valores de g e l que ele deu:
Passo 2
Vamos calcular o momento de inércia I, usando a teoria dos eixos paralelos:
Passo 3
Vamos substituir I:
Dividindo tudo por 17M:
E lembrando da equação do MHS:
Então:
Resposta
Letra F.