Molas e Pêndulos
Um pêndulo físico de massa e momento de inércia , está preso em uma de suas extremidades. O pêndulo sofre então uma leve perturbação externa, tal que ele começa a oscilar em pequenos ângulos devido a um campo gravitacional . Assuma também que o centro de massa do pêndulo está a uma distância do ponto fixo. Qual a frequência angular de oscilação?
Passo 1
Essa é simples! Foi resolvida em nossa teoria. Mas vamos relembrar:
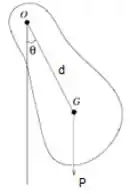
Essa é a figura de nosso pêndulo físico. Ele está submetido a um torque realizado pela força gravitacional com braço de alavanca A segunda lei de Newton para rotações fica:
Que é o torque resultante. Sendo :
Passo 2
Como :
Comparando essa equação com uma equação de MHS, temos que:
Sendo :
Resposta
b)
Exercícios de Livros Relacionados
No exemplo que envolve a Fig. 15-11, vimos que um pêndulo físico em forma de régua possui um centro de oscilação a uma distância 2L/3 do ponto de suspensão. Mostre que a distância entre o ponto de sus
Na Fig. 15-40, o pêndulo é formado por um disco uniforme de raio r = 10,0 c m e 500 g de massa preso a uma barra homogênea de comprimento L = 500 m m e 270 g de massa. (a) Calcule o momento de inércia
Na Fig. 15-47a, uma placa de metal está montada em um eixo que passa pelo seu centro de massa. Uma mola com k = 2000 N / m está ligada a uma parede e a um ponto da borda da placa a uma distância, r =
Um pêndulo é formado suspendendo-se por um ponto uma barra longa e fina. Em uma série de experimentos o período é medido em função da distância x entre o ponto de suspensão e o centro da barra. (a) Se
Na Fig. 15-42, um pêndulo físico é formado por um disco uniforme (de raio R = 2,35 c m ) sustentado em um plano vertical por um pino situado a uma distância d = 1,75 c m do centro do disco. O disco é