Uma roda pode girar livremente em torno do seu eixo fixo. Uma mola de constante k é presa a um dos raios a uma distância R do eixo. Suponha que a roda é um anel de massa m e raio R, cujo momento de inércia é igual a .
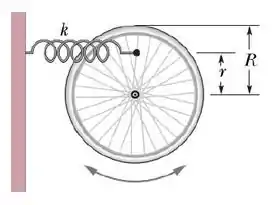
a) Calcule a frequência angular das pequenas oscilações desse sistema, em termos de m, R, r e k.
b) Suponha que o deslocamento angular máximo de um ponto do anel seja e que tem t = 0 s o deslocamento angular desse ponto seja metade desse valor. Escreva a equação do movimento angular do anel.
c) Se o anel tem uma massa m = 3 kg, a constante da mola é k = 100 N/m, = 0,01 rad e , calcule a velocidade angular de um ponto do anel em t = 0 s.
Passo 1
a) Vou considerar que a roda gira um ângulo em torno do eixo fixo. Para pequenos valores de , podemos dizer que a elongação x da mola é:
Escrevendo a segunda lei de Newton para rotações:
Comparando com a equação do MHS:
Tiramos que:
Passo 2
b) A equação do movimento do anel vai ser da forma:
O problema disse que:
Então:
Passo 3
c) A velocidade angular vai ser:
Fazendo algumas continhas achamos:
Resposta
a)
b)
c)