Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulo Físico

Ver Teoria
Exercício 15123456789101112131416171819202122232425262728293031323334

Enunciado

Um pêndulo físico consiste de uma haste rígida delgada, de massa desprezível e comprimento L , sobre a qual duas diminutas partículas estão afixadas, uma de massa m e outra de massa 2 m . As distâncias destas duas massas ao ponto de suspensão são, respectivamente, L e L / 2 . Para pequenas oscilações do pêndulo, podemos afirmar que este desenvolve movimento harmônico, com frequência natural de oscilação:

  1. ω 0 = g 3 L
  2. ω 0 = 2 g 3 L
  3. ω 0 = 4 g 3 L
  4. ω 0 = 2 g L
  5. ω 0 = 8 g 3 L

Passo 1

Fala aee, beleza?

Vamos esquematizar essa questão pra gente entender melhor o que ela está descrevendo:

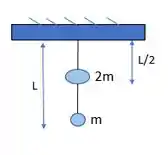
Bem melhor agora, não é? =)

Passo 2

Para pequenas oscilações do pêndulo, podemos afirmar que:

ω = M g d I

Onde d é a distância do centro de massa do sistema ao eixo de rotação. Então, bora calcular onde está esse centro de massa primeiro:

d = 2 m L 2 + m L 2 m + m = 2 L 3

Beleza! Essa é a posição do centro de massa em relação ao eixo de rotação!

Passo 3

Opa, então, temos que:

ω = M g 2 L 3 I

Onde o momento da inércia I é dado por:

I = ∑ m . d 2 = m L 2 + 2 m L 2 2 = 3 m L 2 2

Logo, substituindo na equação, temos:

ω = 3 m g 2 L 3 3 m L 2 2

Simplificando:

ω = 4 g 3 L

Esse é o nosso gabarito!

Resposta

Letra C

Exercícios de Livros Relacionados

No exemplo que envolve a Fig. 15-11, vimos que um pêndulo físico em forma de régua possui um centro de oscilação a uma distância 2L/3 do ponto de suspensão. Mostre que a distância entre o ponto de sus
Na Fig. 15-40, o pêndulo é formado por um disco uniforme de raio r = 10,0 c m e 500 g de massa preso a uma barra homogênea de comprimento L = 500 m m e 270 g de massa. (a) Calcule o momento de inércia
Na Fig. 15-47a, uma placa de metal está montada em um eixo que passa pelo seu centro de massa. Uma mola com k = 2000 N / m está ligada a uma parede e a um ponto da borda da placa a uma distância, r =
Um pêndulo é formado suspendendo-se por um ponto uma barra longa e fina. Em uma série de experimentos o período é medido em função da distância x entre o ponto de suspensão e o centro da barra. (a) Se
Na Fig. 15-42, um pêndulo físico é formado por um disco uniforme (de raio R = 2,35 c m ) sustentado em um plano vertical por um pino situado a uma distância d = 1,75 c m do centro do disco. O disco é