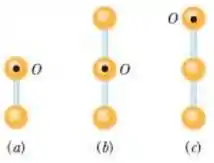
A figura mostra três pêndulos físicos formados por esferas homogêneas iguais, rigidamente
ligadas por barras iguais de massa desprezível. Os pêndulos são verticais e podem oscilar em torno do ponto de suspensão O. Ordene os pêndulos de acordo com o período das oscilações, começando pelo maior.
a) a, c, b;
b) b, a, c;
c) b, c, a;
d) c, b, a;
e) todos empatados;
Passo 1
Num pêndulo físico, o período de oscilação é descrito pela equação:
Onde I é o momento de inércia em relação ao eixo de rotação, m é a massa e h a distância entre eixo de rotação e o centro de massa do sistema.
O momento de inércia em relação a um eixo qualquer, segundo o teorema dos eixos paralelos, é:
Se considerarmos o diâmetro dessas esferas muito pequenos, podemos considerar seu momento de inércia desprezível e fazer a seguinte aproximação:
Passo 2
Em (a),
O centro de massa está no centro da barra que une as duas esferas, se o comprimento da esfera é L, então, . O momento de inércia da esfera que está no eixo de rotação é zero, e como a outra está a uma distância L, então:
Então, como a massa total é (2m),
Em (b), como o centro de massa coincide com o eixo de rotação, então , os torques se anulam, o que faz com que o período:
Ele levaria um tempo infinito para completar uma volta, ou seja, o pêndulo não oscila.
Em (c), o centro de massa está a uma distância L do eixo de rotação, então . O momento de inércia do sistema será a soma dos momentos de inércia das duas esferas (a ligada ao ponto fixo é zero)
Juntando tudo,
Resposta
c) b, c, a;