Cada um dos dois pêndulos mostrados na figura abaixo consiste em uma esfera sólida uniforme de massa sustentado por uma corda de massa desprezível, porém a esfera do pêndulo é muito pequena, enquanto a esfera do pêndulo é bem maior. Sejam e os tempos que cada pêndulo demora em completar uma oscilação. Para deslocamentos pequenos, pode-se dizer que: Dados: Momento de inércia de uma esfera (a partir de um eixo de simetria): Teorema dos eixos paralelos:
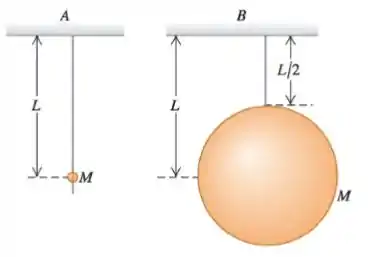
O pêndulo demora mais tempo que o pêndulo em completar uma oscilação, com .
Os dois pêndulos levam o mesmo tempo para completar uma oscilação, com .
O pêndulo demora menos tempo que o pêndulo em completar uma oscilação, com .
O pêndulo demora mais tempo que o pêndulo em completar uma oscilação, com / .
O pêndulo demora menos tempo que o pêndulo em completar uma oscilação, com .
Passo 1
Bem, vimos na teoria de pêndulos simples que existe uma fórmula para calcular o período de oscilações de um pêndulo quando a carga pode ser considerada um ponto, lembra?
A fórmula é
Então o tempo de oscilação depende apenas da gravidade e do comprimento da corda, assim
Temos que
Enquanto isso, o pêndulo , não pode ser considerado um ponto, então chamamos ele de pendulo físico, e temos a seguinte fórmula
Usando os dados que ele deu para calcularmos o momento de inércia
Assim, chegamos a conclusão que
Resposta
Alternativa