Na figura, o pêndulo é formado por um disco uniforme de raio e de massa preso a uma barra uniforme de comprimento e massa .
- Calcule o momento de inércia em relação ao ponto de suspensão.
- Qual é a distância entre o ponto de suspensão e o centro de massa do pêndulo?
- Calcule o período de oscilação.
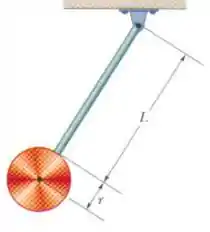
Dados:
Momento de inércia de centro de massa de um disco de massa
Momento de inércia de centro de massa de uma barra de massa :
Gravidade:
Passo 1
a):
Vamos olhar o esquema abaixo:
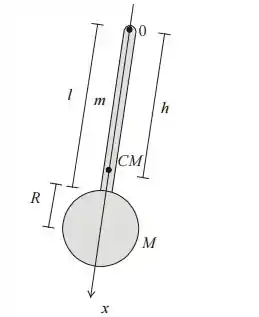
Como você pode ver, o vai estar mais deslocado pro circulo.
Passo 2
Bora calcular o momento de inércia do conjunto em relação ao ponto de rotação. O momento de inércia vai ser a soma dos momentos de inércia da barra e do círculo:
Como o eixo de rotação não passa por cima de nenhum dos centros de massa, teremos que usar o teorema dos eixos paralelos em cada caso.
Primeiro a barra:
Perceba que a distância do centro de massa da barra até o eixo de rotação é
Agora o do círculo:
Sacou? Percebeu que a distância do centro do disco até o eixo é o comprimento da barra mais o raio do círculo?
Beleza, então:
Assim:
Passo 3
b):
Vamos calcular agora a posição do centro de massa do pêndulo. Se você não lembra muito bem desse assunto, dê uma olhada no nosso conteúdo de Física 1 (:
O centro de massa será dado por:
A gente tá tomando a origem como sendo o ponto de rotação. Se liga nisso (:
Além disso, cada de cada objeto é a posição do centro de massa do mesmo em relação ao ponto de rotação.
Assim:
Como a gente tinha visto, a posição do centro de massa está bem deslocado pra posição do círculo.
Passo 4
c):
Agora que a gente já calculou tudo que tínhamos que calcular, fica fácil calcular o período de oscilação. Só a gente aplicar a fórmula:
Onde é o peso do corpo todo e a distância do centro de massa do corpo até o ponto de rotação.
No caso, como calculamos o centro de massa em relação ao centro de rotação, o vai ser o próprio valor da posição
E o peso vai ser dado por:
E como:
Podemos aplicar todos os valores na equação do período:
Resposta
a):
b):
c):