Um haltere de comprimento é formado por uma haste de massa desprezível e duas esferas de massa . O haltere pode girar livremente em torno do ponto , formando um ângulo em relação à horizontal. Uma mola, de constante elástica está conectada a uma distância do ponto e encontra-se relaxada (nem comprimida nem esticada) quando o ângulo é zero. Considerando pequenos valores de , obtenha:
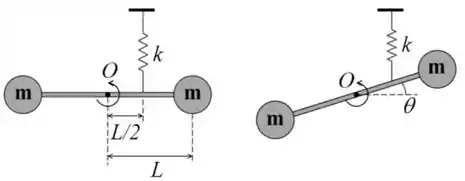
(a) A equação diferencial que rege o comportamento oscilatório do haltere.
(b) A frequência natural de oscilação do haltere. Expresse a resposta em termos de , e .
Passo 1
Temos que essa mola irá exercer um torque. Tomando como positivo a direção anti-horária o torque é dado por
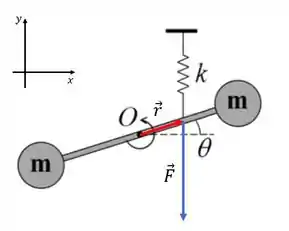
O ângulo entre os vetores e é
Pela figura temos que a distensão da mola é dada por
Assim
Podemos usar a seguinte identidade trigonométrica para rescrever esse último seno menos simpático
De forma que
Assim temos o torque dado por
Passo 2
Agora temos que fazer a aproximação para ângulos pequenos. Vamos expandir o seno e o cosseno até termos lineares em
Assim a intensidade do torque fica
Definindo como positivo o eixo saindo da folha, temos que pela regra da mão direita que o torque aponta para dentro da folha, de forma que
Passo 3
Já a segunda lei de Newton para rotações nos diz que
Temos que
E o momento de inercia do haltere é dado por
Assim
E essa equação diferencial para
Passo 4
A equação obtida é a equação de um oscilador harmônico em .
Essa equação pode ser reescrita como
Onde podemos identificar a frequência como