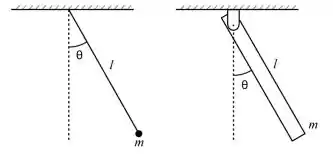
Considere os dois tipos de pêndulos ilustrados ao lado: o primeiro sendo um pêndulo simples e o segundo um pêndulo físico (com momento de inércia igual a em relação à extremidade superior). Julgue as afirmações abaixo, relativas ao movimento de ambos os pêndulos:
) Se considerarmos o regime de oscilações pequenas, ambos os pêndulos descrevem um movimento harmônico simples.
) O período dos dois pêndulos será o mesmo se ambos tiverem a mesma massa e o mesmo comprimento.
) Quanto menor é o ângulo de oscilação de cada pêndulo, menor fica o seu período.
(A) Apenas as afirmações , e estão corretas.
(B) Apenas as afirmações e estão corretas.
(C) Apenas as afirmações e estão corretas.
(D) Apenas a afirmação está correta.
(E) Apenas a afirmação está correta.
Passo 1
Temos dois pêndulos, um deles simples e o outro físico.
No pêndulo simples, temos a massa concentrada na extremidade do fio, sendo considerada como uma partícula.
Já no pêndulo físico, temos a massa distribuída ao longo do corpo e isso gera algumas diferenças entre eles.
Vamos analisar as afirmativas.
Passo 2
) Se considerarmos o regime de oscilações pequenas, ambos os pêndulos descrevem um movimento harmônico simples.
Isso é verdadeiro, pois, independente se o pêndulo for simples ou físico, ele realiza um movimento oscilatório, ou seja, um movimento em que as propriedades (posição , velocidade , aceleração ...) se repetem com o tempo (MHS).
Afirmativa está correta.
Passo 3
) O período dos dois pêndulos será o mesmo se ambos tiverem a mesma massa e o mesmo comprimento.
Bom, aqui temos que comparar o período dos dois pêndulos, então vamos utilizar as expressões para o cálculo do período de cada um deles.
Para um pêndulo simples, temos que o período, que chamaremos de é dado por:
Onde é o comprimento do fio do pêndulo.
Como o comprimento do fio é , ficamos com:
Agora vamos ao pêndulo físico, seu período, que chamaremos de , é dado por:
Onde é o momento de inércia com relação ao ponto por onde passa o eixo de rotação e é a distância desse mesmo ponto ao centro de gravidade da barra.
O enunciado deu que o momento de inércia com relação à extremidade superior (eixo de rotação) é . Além disso, seu centro de gravidade está localizado na metade da barra, logo a distância é igual à :
Assim, temos que o período é diferente do período .
A afirmativa está incorreta.
Passo 4
) Quanto menor é o ângulo de oscilação de cada pêndulo, menor fica o seu período.
Novamente, vamos olhar para as expressões dos períodos:
Podemos ver que elas não dependem do ângulo ...
Isso acontece em qualquer pêndulo que realiza oscilações com ângulos não muito grandes. Seu período se mantém o mesmo para qualquer que seja o ângulo de oscilação (desde que não muito grandes, já que usamos a aproximação para ângulos pequenos).
A afirmativa está incorreta.
E assim, ficamos com a alternativa (E).
Resposta
Letra (E)