Desenvolva o quadrado do binômio abaixo
Passo 1
Opa!! Esse exercício podemos resolver de duas formas: Na primeira faremos a multiplicação na mão e na segunda utilizaremos os Produtos notáveis, beleza?! Vamos ver que nas duas formas chegaremos no mesmo resultado!

Passo 2
Queremos desenvolver o binômio
Certo?! Vamos primeiro fazer a multiplicação na mão! Se você reparar, quando escrevemos o que no fundo estamos querendo fazer é
Isso porque qualquer coisa elevada ao quadrado é ela multiplicada por ela mesma.
Concorda?!
Então vamos fazer a multiplicação de cada um dos termos. Para isso, podemos utilizar o chuveirinho:
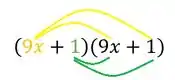
Onde multiplicamos cada termo do primeio parênteses com cada termo do segundo.
Ao realizarmos essa multiplicação, teremos
![]()
Fazendo as continhas, ficamos com
![]()
Somando os termos que tem
![]()
Beleza?! Ou seja, ao desenvolver o binômio, temos
![]()
Agora vamos resolver essa mesma questão utilizando Produtos Notáveis??
Passo 3
Um dos casos mais comuns de produtos notáveis é o quadrado da soma de dois termos:
Que pode ser feito nesse formatinho aqui:
Onde essa igualdade sempre será verdadeira! Ou seja, se tivermos uma expressão do tipo , isso é a mesma coisa que e vice-versa! Beleza?!
Vamos utilizar essa igualdade então pra resolver nosso exercício! Vamos fazer tudo bem detalhadinho pra ninguém ficar pra traz! Bora lá!
Se você reparar, do lado esquerdo da equação temos o quadrado da soma de dois termos:
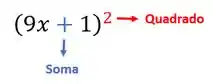
Assim, podemos utilizar o produto notável!! Ficará assim:
No nosso problema quem está no lugar do é o , e quem está no lugar do é o . Assim, vamos escrever o lado direto do produto notável no mesmo formado, substituindo quem é o e quem é o :
![]()
Beleza?! Agora vamos fazer as contas do lado direito da equação:
![]()
E assim chegamos no nosso resultado!!
Se voce reparar foi o mesmo resultado que encontramos ao fazer a multiplicação na mão!
Show de bola?!