O produto é igual a:
Passo 1
Vamos lááá!! Para resolver essa questão a primeira coisa que precisamos reparar é que temos o produto de uma soma e uma diferença, concorda?!
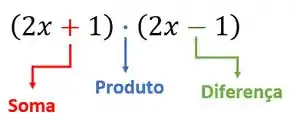
Temos duas formas de atacar essa questão! Faremos das duas formas aqui: Primeiro faremos a multiplicação na mão mesmo e depois faremos utilizando os Produtos Notáveis, beleza?!

Passo 2
Primeiro vamos fazer a multiplicação na mão! Para isso, utilizaremos o chuveirinho!! Como funciona? Se liga!
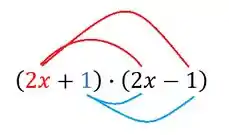
Fazendo a multiplicação, teremos
![]()
Show de bola?! Ficou grandinho mas dá pra arrumar e simplificar a nossa vida! Vamos fazer as continhas do lado direito da equação:
![]()
Beleza?! Se você reparar podemos cortar o com o :
![]()
E assim temos o resultado do nosso produto!
![]()
Passo 3
Beleza... e qual é a outra forma que temos de resolver esse problema???

Lembra que eu disse que temos o produto de uma soma e uma diferença??
A outra forma que iremos resolver é usando Produtos Notáveis!!

Ó, um dos casos mais comuns de produtos notáveis é essa aqui embaixo:
Onde essa igualdade sempre será verdadeira! Ou seja, se tivermos uma expressão do tipo , isso é a mesma coisa que e vice-versa! Beleza?!
Vamos utilizar essa igualdade então pra resolver nosso exercício! Vamos fazer tudo bem detalhadinho pra ninguém ficar pra traz! Bora lá!
Se você reparar, do lado esquerdo da equação temos o produto de uma soma e uma diferença, igual ao nosso enunciado:
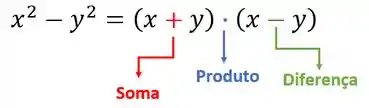
Como o expressão do nosso exercício também é o produto de uma soma e uma diferença, podemos utilizar essa igualdade!
Então faremos a diferença do quadrado do primeiro e do segundo termo:

E assim chegamos no nosso resultado,
![]()
Que se você reparar é o mesmo resultado que encontramos anteriormente!
Show de bola?!