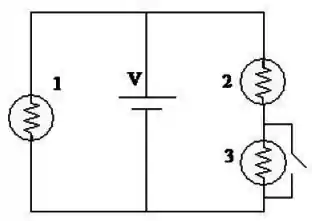
Uma bateria ideal é conectada a três lâmpadas idênticas, como mostrado na figura abaixo. Um interruptor em paralelo com a lâmpada 3 está originalmente aberto e é depois fechado. Quando o interruptor está fechado, o que acontece com o brilho das lâmpadas 1 e 2?
- 1 clareia, 2 clareia
- 1 escurece, 2 permanece inalterada
- 1 permanece inalterada, 2 permanece inalterada
- 1 permanece inalterada, 2 brilha mais
- 1 permanece inalterada, 2 escurece
Passo 1
Para resolvermos esse problema, é importante que a gente ache quais são os valores das correntes que passam por cada um dos resistores antes e depois que o interruptor é fechado.
Mas por que isso? Bom, a gente sabe que a potência (=energia por unidade de tempo) que um resistor dissipada quando é percorrido por uma corrente é dada por:
e essa quantidade que está relacionada com o “brilho” das lâmpadas, ok?
Precisamos ver, então, como são as potências dissipadas por cada lâmpada antes e depois de o interruptor se desligado.
Antes disso, “desligar o interruptor” significa fechar aquela chave que está em paralelo com o resistor 3. Quando essa chave é fechada, não passa mais corrente no resistor 3 e a “luz” dessa lâmpada se apaga, ou seja, ela não dissipada mais energia. Nesse caso, a corrente passa por dentro da chave e é a mesma que passa pelo resistor da lâmpada 2.
Vamos lá!!??
Passo 2
Agora, vamos analisar apenas as correntes em cada caso.
ANTES DE O INTERRUPTOR SER FECHADO:
A corrente que passa na resistência da lâmpada 1 será:
A corrente que passa nos resistores e (que estão em série) é:
DEPOIS DE O INTERRUPTOR SER FECHADO:
A corrente que passa em é a mesma, já que a lâmpada é a mesma e está ligada à mesma tensão .
Agora, a corrente que passa por será:
ou seja, a nova corrente é maior do que a anterior: .
Passo 3
Se analisamos agora as potências dissipadas, vemos que o “resistor dissipa mesma potência de antes”, já que por ele passa a mesma corrente . Por isso, a lâmpada 1 tem o mesmo “brilho” depois que o interruptor está fechado.
Já em passa uma corrente maior e, por isso, a potência dissipada através dele também será maior depois que o interruptor é fechado:
Então, lembre-se: brilho de uma lâmpada tem a ver com a potência (energia por unidade de tempo!) que é dissipada por sua resistência quando passa uma corrente por ela.
Resposta
Letra d.