UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 1a
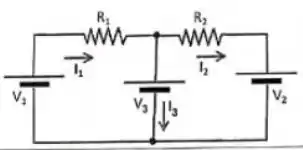
Encontre a expressão literal para as correntes do circuito, considerando as direções das correntes dadas na figura.
- Calcule o valor da corrente considerando os valores de e
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá? Na letra (a) o problema pede para calcularmos a corrente , que é que passa pela fonte . Para resolver esse tipo de questão, precisamos aplicar a lei das malhas e a lei dos nós nesse circuito para termos equações suficientes para resolver para .
mas calma, vou fazer passo a passo com você!
Passo 2
Começando pela lei dos nós! Vamos olhar para o circuito, naquele nozinho lá em cima, bem no meio, onde o fio que sai do resistor se divide em dois:
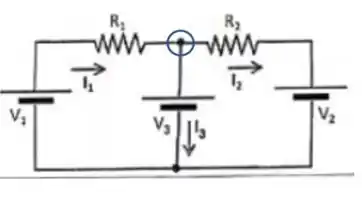
Caso o sentido esteja errado, vamos encontrar naturalmente. Nesse caso, a corrente achada seria negativa. Beleza? Se o sentido que supomos agora estiver correto, todas as correntes serão positivas.
Passo 3
Agora vamos aplicar a lei das malhas. Ela nos diz que para um caminho fechado, a diferença de potencial é zero. Então a ideia é percorrer um caminho fechado, adicionando as contribuições dos resistores ( se estiver no sentido da corrente) e fontes ( se for no sentido positivo da fonte – da placa menor para a maior) e igualar a zero.
Escolhendo o caminho que passa pela fonte e e pelo resistor
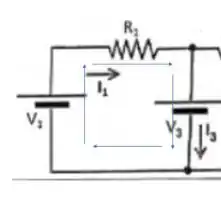
Admitindo o sentido do desenho, esse caminho vai nos dar a seguinte equação:
Beleza?
E precisamos de outra equação, uma que envolva , pois a equação das correntes envolve as três (e para letra (b) vamos precisar de , então já vamos nos adiantar!).
Passo 4
Agora considerando o caminho da malha mais de fora, que passa pelos resistores e pelas fontes e
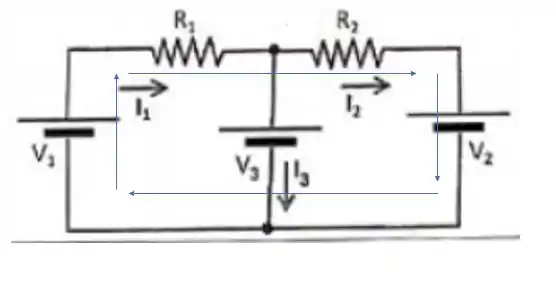
A equação da lei das malhas fica assim:
Pronto! Temos 3 equações, e 3 variáveis! Agora é “só” resolver
Com essas equações temos um sistema:
Da equação (2):
Os valores dados são:
Assim a corrente é:
Passo 5
Agora podemos encontrar as outras correntes!
Da equação (3):
Os valores que faltam são e , agora é só substituir:
O sinal negativo da corrente significa que fornece corrente para o nó, e não sai dele!
E da primeira equação podemos determinar a corrente :
Assim temos que o sentido de está correto com o que supomos lá no começo. O único sentido equivocado é o da corrente . O sentido correto das correntes é esse aqui:
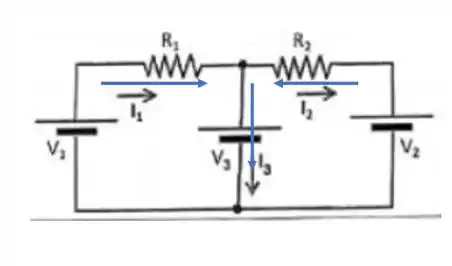
Mas você não precisa se preocupar! O módulo da corrente é o que nos interessa! E o sinal negativo só nos indica que o sentido que escolhemos lá no início não é o correto, mas não muda nada no resultado, ta bem?
Espero ter te ajudado!