Determine na figura ao lado a corrente em cada resistor e a diferença de potencial entre os pontos e .
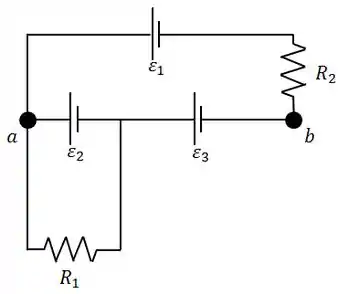
Considere , , , e . Suponha que a bateria não possui resistência.
Passo 1
Pra começar, vamos adotar um sentido arbitrário para a corrente do circuito, aí conforme formos calculando os valores das correntes em cada resistor, existem duas possibilidades:
- Se o valor da corrente for positiva, significa que o sentido que escolhemos estava certo!
- Se o valor da corrente for negativa, significa que o sentido que escolhemos estava errado...


Mas não precisa se preocupar em voltar e corrigir, uma vez que você deixou claro o sentido que você escolheu, encontrar um valor negativo pra corrente não tem problema.
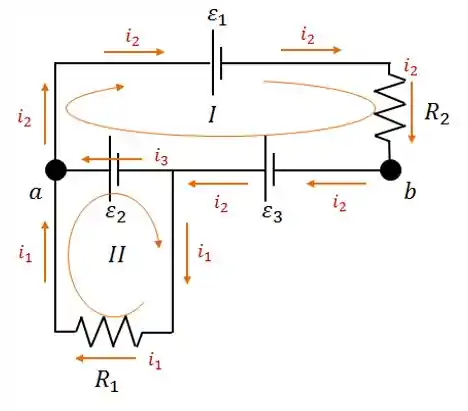
Bom, o sentido que vamos escolher é esse aqui:
Passo 2
Vamos analisar cada malha separadamente, beleza?
Antes de começar, vale lembrar que, quando a corrente passa por uma FEM, existem duas possibilidades:
- Se ela passar primeiro pela barra menor e depois pela barra maior, a voltagem vai ser positiva;
- Se ela passar primeiro pela barra maior e depois pela barra menor, a voltagem vai ser negativa;
Agora sim, vamos lá!
Passo 3
Malha I:
Onde:
;
;
;
;
Logo:
Passo 4
Malha II:
Onde:
;
;
Logo:
e o sinal negativo aqui significa que escolhemos o sentido dessa corrente contrário ao correto, mas o módulo da corrente é, de fato, .
Passo 5
A voltagem entre os pontos e é dada por:
Onde:
;
;
Logo: