UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 1b
Encontre a expressão literal para as correntes do circuito, considerando as direções das correntes dadas na figura.
- Calcule o valor da corrente considerando os valores de e
- Calcule a potência dissipada em , para os mesmos valores acima.
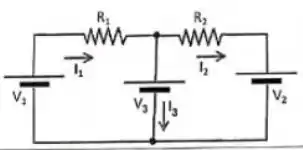
Passo 1
Oi, tudo bem?
No item anterior dessa questão foi pedido o valor da corrente . E para isso foram aplicadas duas leis: dos nós e das malhas.
Assim foram determinadas as correntes:
A corrente :
E a corrente :
Beleza?
E o sentido? O sentido encontrado foi o desenhado aqui embaixo:
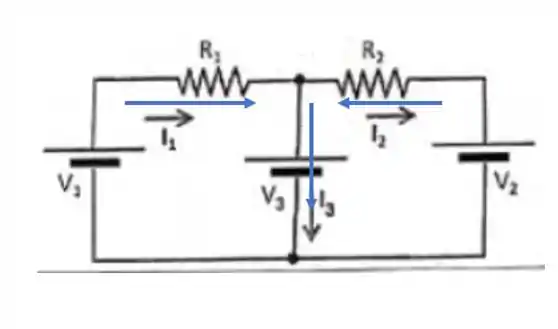
Mas independente do sentido, a potência dissipada pelo resistor é dada por:
Então agora, para resolver a letra (b), é só aplicar os valores de resistência e de corrente na fórmula da potência e correr para o abraço!
Passo 2
A corrente e a resistência , agora é só substituir:
Beleza? É só isso mesmo!
Ufa! Vamos para a próxoma?
Resposta
Exercícios de Livros Relacionados
Verifique seus resultados para o Problema 79 usando os seguintes valores específicos: (a) R1 = 4,00 Ω, R2 = 6,00 Ω; (b) R1 = 4,00 Ω, R3 = 3,00 Ω; e (c) R2 = 6,00 Ω, R3 = 3,00 Ω.
Um comprimento de arame tem uma resistência de 120Ω . O arame é cortado em pedaços que têm o mesmo comprimento, e então os arames são conectados em paralelo. A resistência do arranjo paralelo é de 1,8
(a)Resistência a resistência equivalente entre os pontos a e b na Figura 26-56. (b) Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
(a)Determine a resistencia equivalente entre os pontos a e b na figura 25.57. (b)Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
Quatro resistores de 18,0 Ω são ligados em paralelo a uma fonte ideal de 25,0 V. Qual é a corrente na fonte?