O circuito ilustrado na figura abaixo é composto por três baterias ideais, e cinco resistores ôhmicos. Considerando tal circuito, calcule:
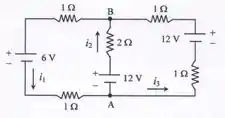
- As intensidades das correntes elétricas , e .
- O valor absoluto da diferença de potencial entre os pontos e , ou seja, .
Passo 1
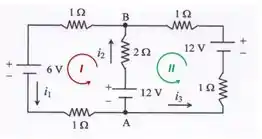
a) A primeira coisa que precisamos fazer em circuitos desse tipo é definir os sentidos das malhas e das correntes. Bom, o sentido das correntes já foi dado pelo problema, então vamos colocar os sentidos das malhas.
Como está na figura abaixo, vamos colocar as malhas e no sentido anti-horário. Depois disso, vemos que temos três variáveis, as correntes, então precisamos de três equações. Vamos atrás delas agora...
O problema também já forneceu indicou os nós e , então vamos começar pela lei dos nós. Para o nó , temos:
Agora, aplicando e lei das malhas para a malha :
que vai dar no seguinte:
Falta uma equação. Para encontrá-la, aplicamos a lei das malhas para a malha :
que é a nossa última equação do sistema:
Pegando a segunda equação acima e fazendo e jogando isso mais na primeira equação, vamos ter que:
Portanto, substituindo isso na primeira ou segunda equação do nosso sistema, teremos
Passo 2
b) Para encontrar essa diferença de potencial entre os pontos e da figura, podemos escolher qualquer trajeto entre esses pontos. Poderíamos, por exemplo, percorrer qualquer uma das malhas saindo de em direção a .
Mas podemos também pegar o trecho que passa pelo meio do circuito e vamos utilizar este. Se o ponto tem um potencial e o ponto tem um potencial , então, partindo do ponto e percorrendo o trecho em direção a , vamos ter
Nesse tipo de problema, não se esqueça, você pode escolher o trecho que quiser entre os pontos e para encontrar a diferença de potencial entre dois pontos quaisquer do circuito.