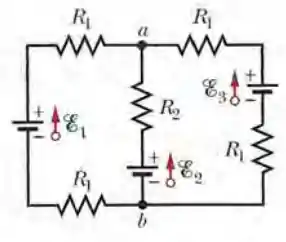
(Cap 27.7 – 45) Na Fig. 27-54, as resistências são e e as forças eletromotrizes das fontes ideais são , e . Determine (a) o valor absoluto e (b) o sentido (para cima ou para baixo) da corrente na fonte 1; ( c) o valor absoluto e (d) o sentido da corrente na fonte 2; (e) o valor absoluto e (f) o sentido da corrente na fonte 3; (g) a diferença de potencial

Começando pelo item (a), o que vemos acontecer no ramo onde temos a fonte de tensão 1?

Vamos notar aqui que existem dois resistores em série em cada ramo do circuito, que contribuem com uma resistência total para o ramo correspondente. Como e , as correntes em e 2 e e 3 são iguais: . Assim, a corrente em e 1 é . Nesse caso, e, portanto,

Assim, a corrente em e é

Pro item (a) era isso! Bem simples não é mesmo?

Levando em consideração a avaliação feita no passo anterior, e o esquema do circuito, no item (b) podemos afirmar que o sentido de é para baixo (ou anti-horario).

Partindo para o item (c), no passo 2 fizemos a análise do circuito e chegamos à conclusão que: . E como naquele mesmo passo já encontramos o valor de , podemos afirmar que:

A corrente em é

Por analogia, na questão (d) temos que: o sentido de é para cima (ou horário).

Partindo para o item (e), novamente vamos usar a análise feito no passo 2, em que chegamos à conclusão que: . E como naquele mesmo passo já encontramos o valor de , podemos afirmar que:

(e) A corrente em e é:

(f) O sentido de é para cima (ou horario).

Por fim, para resolvermos o último item, podemos observar no circuito que: e que . Note que em o sinal é negativo devido ao sentido da corrente.

Então, podemos dizer que:

Ufa! Terminamos! Pra essa questão é isso pessoal! Bora pra mais uma?