Livro Halliday, Volume 3, 9ª edição, Capítulo 27, Seção 7, Exercício 40
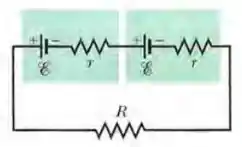
(Cap. 27.7 - Ex.40) Duas fontes iguais de força eletromotriz e resistência interna podem ser ligadas a uma resistência em paralelo (Fig. 27-50) ou em série (Fig. 27-51). Se , qual é a corrente na resistência R (a) no caso da ligação em paralelo; (b) no caso da ligação em série? (c) Em que tipo de ligação a corrente é maior? Se , qual é a corrente na resistência (d) no caso da ligação em paralelo; (e) no caso da ligação em série? (f) Em que tipo de ligação a corrente é maior?
Passo 1
Faaaala, galerinha! Tudo certo? Bora lá resolver mais uma questão?
Essa é uma questão bem típica de circuito em que devemos analisar as diferentes malhas de acordo com a informação que está sendo pedida em cada item. Então vamos lá analisar cada caso separadamente.
Começando pelo item (a), quando a ligação está em paralelo, a corrente nas fontes é igual. E, portanto, a corrente no resistor se dá por: .
Assim, vamos utilizar a lei das malhas para calcular a corrente :
Pronto! Agora vamos utilizar essa relação encontrada na fórmula da corrente no resistor estabelecida ali em cima:
Substituindo os valores, vamos ter então:
Passo 2
Partindo para o item (b), no caso onde as fontes estão postas em série, todas as resistências estão em série e o valor das forças eletromotrizes se soma, portanto:
Passo 3
Para o item (c), temos que comparando os itens (a) e (b), vemos que na ligação em série a corrente é maior.
Passo 4
Já no item (d), temos que a corrente para a ligação em paralelo é:
Passo 5
(e) Temos que a corrente para a ligação em série é:
Passo 6
(f) Comparando os itens (d) e (e), vemos que a ligação em paralelo maior valor de corrente.
Prontinho, pessoal! O enunciado assusta, mas vemos que é bem tranquilo!
Bora lá resolver mais uma questão?
Resposta
(a)
(b)
(c) Em série.
(d)
(e)
(f) Em paralelo.