No circuito indicado na Figura abaixo, calcule:
- a corrente no resistor de ;
- a fem e a fem ;
- a resistência .
Observe que foram fornecidas os valores de três correntes.
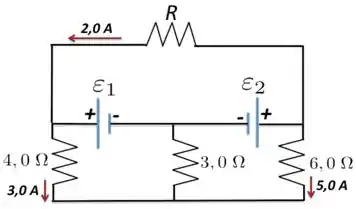
Passo 1
a) Como o exercício deu para gente três valores de corrente, bem como o sentido delas, ficou mais fácil para descobrirmos os valores das outras. Dá uma olhada na Figura abaixo.
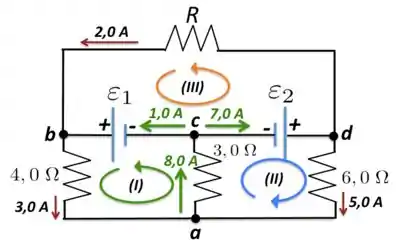
Antes de olharmos para as malhas, considere primeiro o nó da Figura. Nesse ponto, chega a corrente de valor e sai outra de . Portanto, no sentido do ponto para , deve chegar outra corrente de valor . Blz?
Agora, olhando para o nó , saem desse ponto, duas correntes, uma de e outra de . Portanto, no sentido de para , tem uma corrente de . Tranquilo?
Olhando para o nó , saem as correntes e . Isso nos leva a concluir que de para , tem uma corrente cujo valor é . Essa é a corrente que passa no resistor de .
Passo 2
b) Vamos considerar a malha em verde na Figura acima. Percorrendo essa malha, no sentido anti-horário, partindo do nó e voltando a esse mesmo nó, teremos
Dessa expressão, a gente tira que:
Agora para a malha em azul na Figura acima, partindo do nó e volto para esse mesmo nó, termos que
que tem como resultado
Passo 3
c) Para obtermos a resistência , precisamos, agora, da malha representada em laranja na Figura acima. Saindo do ponto e voltando para esse mesmo ponto, teremos o seguinte:
Resolvendo essa equação, temos que
Resposta
- ;
- ;