UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 1c
Calcule a potência dissipada em considerando e
Passo 1
Oi, tudo bem?
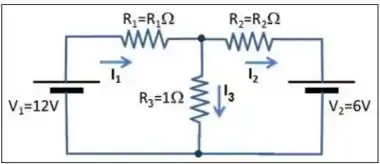
Nas letras (a) e (b) o problema pede para calcularmos as correntes e , que são as que passam pela fonte e pelo resistor . Para resolver esse tipo de questão, aplicamos a lei das malhas e a lei dos nós no circuito, para termos equações suficientes para resolver as correntes.
Resgatando o sistema feito nos itens anteriores, o sistema de equações ficou assim:
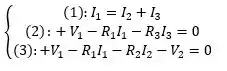
Agora o problema pede para acharmos a potência dissipada no resistor . Bom, para isso precisamos lembrar da relação entre potência, resistência e corrente:
Então precisamos do valor da corrente E como temos o valor de , podemos achar pela primeira equação do sistema!
Passo 2
Logo:
A corrente negativa indica que o sentido que adotamos no desenho está incorreto. Mas fique tranquilo, isso não influencia em nada no valor final!
Passo 3
Agora a potência dissipada é:
E é isso!
Espero ter ajudado!