O circuito elétrico ilustrado na figura abaixo apresenta dois geradores ideais e três resistores.
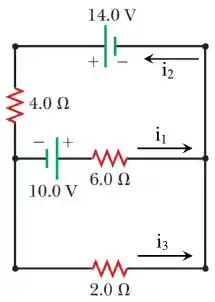
Para tal circuito, calcule em detalhe os valores das correntes elétricas indicadas na figura:
;
;
;
Passo 1
Beleza, vamos começar dando nome aos nós pra conseguirmos analisar melhor esse circuito:
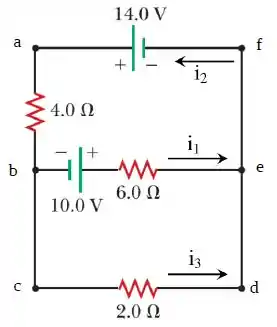
De acordo com a Lei dos Nós de Kirchhoff, o somatório das correntes que entram em um nó deve ser igual ao somatório das correntes que saem do nó.
Assim, se aplicarmos essa lei ao nó , teremos:
Passo 2
Vamos chamar de malha 1 a malha de cima composta pelos pontos , , e , de malha 2 a malha de baixo composta pelos pontos , , e .
De acordo com a Lei das Malhas de Kirchhoff, ao percorrermos uma malha, a soma de todas as diferenças de potencial deve ser nula.
Obs.: O sentido que escolhermos para percorrer a malha é aleatório e não interfere nos resultados, desde que obedeçamos às regras.
Assim, aplicando a Lei das Malhas na malha 1, percorrendo-a no sentido anti-horário, teremos:
Passo 3
Aplicando a Lei das Malhas na malha 2, percorrendo-a no sentido horário, teremos:
Obs.: A diferença de potencial ao passar pelo resistor de ficou positiva porque, ao passar pelo resistor, estávamos percorrendo a malha no sentido oposto ao da corrente .
Passo 4
Agora temos um sistema com 3 equações e 3 variáveis, se liga:
Substituindo da primeira na segunda
Olhando a terceira
Substituindo no que acabamos de achar
Passo 5
Assim como
E olhando a primeira equação
Resposta
;
;
;