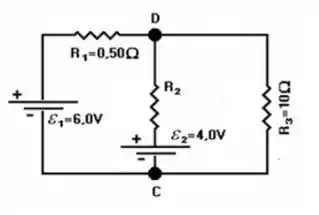
Considere o circuito representado esquematicamente na figura a seguir. A corrente que passa pelo resistor é de e a corrente que passa pelo resistor é de . Os valores das resistências dos resistores e e das forças eletromotrizes e ideais são indicados na figura. Determine o valor do resistor desconhecido .
(a) .
(b)
(c)
(d)
(e)
Passo 1
Vamos supor que a corrente no resistor está indo pra direita e que as correntes nos resistores e estão indo para baixo
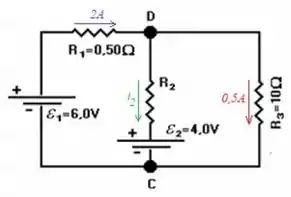
No nó do circuito, podemos ver que:
Passo 2
Agora, calculamos a diferença de potencial entre os nós e como:
Passo 3
Por fim, calculamos como:
Resposta
(a) .
Exercícios de Livros Relacionados
Verifique seus resultados para o Problema 79 usando os seguintes valores específicos: (a) R1 = 4,00 Ω, R2 = 6,00 Ω; (b) R1 = 4,00 Ω, R3 = 3,00 Ω; e (c) R2 = 6,00 Ω, R3 = 3,00 Ω.
Um comprimento de arame tem uma resistência de 120Ω . O arame é cortado em pedaços que têm o mesmo comprimento, e então os arames são conectados em paralelo. A resistência do arranjo paralelo é de 1,8
(a)Resistência a resistência equivalente entre os pontos a e b na Figura 26-56. (b) Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
(a)Determine a resistencia equivalente entre os pontos a e b na figura 25.57. (b)Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
Quatro resistores de 18,0 Ω são ligados em paralelo a uma fonte ideal de 25,0 V. Qual é a corrente na fonte?