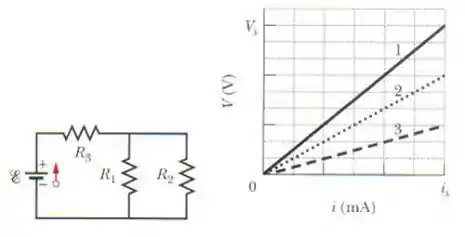
A fonte ideal da figura da esquerda tem uma força eletromotriz de . A curva 1 da figura da direita mostra a diferença de potencial entre os terminais do resistor 1 em função da corrente no resistor. A escala do eixo vertical é definida por e a escala no eixo horizontal é definida por . As curvas 2 e 3 são gráficos semelhantes para os resistores 2 e 3. Qual é a corrente no resistor 2?
Passo 1
Bem. Primeiro temos que entender o que é porquê de a questão querer que a gente use o gráfico do lado direito.
Ele dá um gráfico de . Se calculássemos a área abaixo do gráfico, teríamos a potência, certo? Já que .
Se calculássemos a reta tangente encontraríamos a resistência, já que .
É interessante usar a potência, nessa questão? Acho que não, né?
Mas o valor das resistências podem nos ajudar bastante a resolver essa questão. Vamos calcula-las?
Passo 2
Passo 3
Agora a gente deve chutar um sentido pra corrente. Vou chutar esse aqui!
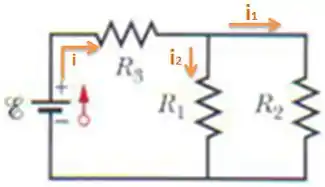
Usando a Lei das Malhas,na malha da direita, teremos:
Passo 4
Agora, aplicando a Lei dos Nós no nó que fica logo após , teremos:
Mas, pera! Quem é ?
Da pra calcular com a resistência equivalente!
Passo 5
Assim, pela Lei de Ohm, teremos:
Agora puxando a equação da Lei dos nós, teremos:
Mas também sabemos que: