Calcule a corrente abaixo considerando os valores de e
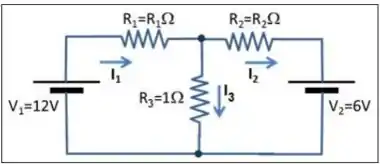
Passo 1
Oi, tudo bem?
Na letra (a) o problema pede para calcularmos a corrente , que é que passa pela fonte . Para resolver esse tipo de questão, precisamos aplicar a lei das malhas e a lei dos nós nesse circuito para termos equações suficientes para resolver para .
Resgatando o sistema feito no item (a), o sistema de equações ficou assim:
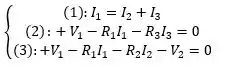
É a partir da segunda equação que vamos determinar a corrente !
Passo 2
A segunda equação é
Os valores dos componentes são
Agora é só substituir:
E é isso!

Espero ter ajudado!