No circuito indicado na Figura abaixo, determine:
- a corrente em cada ramo;
- a diferença de potencial do ponto em relação ao ponto .
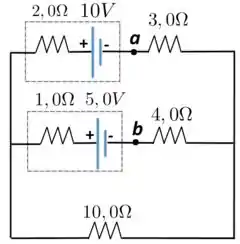
Passo 1
a) Nesse exercício, precisamos encontrar o valor das três correntes , e mostradas na Figura abaixo. Por isso, temos que ter também três equações.
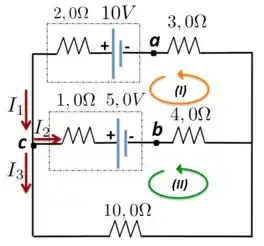
Colocamos as correntes no sentido indicado, como chegando no nó e e saindo desse nó, de maneira que a gente tenha, a partir da lei dos nós, que:
Agora tomando a malha indicada, que está no sentido anti-horário, saindo do nó e voltando para esse ponto, teremos:
Reorganizando essa equação
Aplicando a leis das malhas para a malha , de novo saindo do nó e voltando a esse ponto, chegamos a
Portanto, o sistema que a gente tem que resolver é o seguinte:
Passo 2
a) Continuando...
Vamos resolver o sistema acima. Se substituímos a primeira equação na segunda, obtemos as duas equações abaixo
Multiplicando a primeira equação acima por 2 e somando com a segunda equação, vamos ter que:
Substituindo esse valor na primeira das equa�es acima, tiramos o valor da corrente
Como , então
Passo 3
b) Partindo do ponto indicado na Figura, até o ponto , no sentido anti-horário e tomando a malha, teremos que
Substituindo os valores que encontramos para as correntes,