Calcule a potência dissipada em considerando e

Oi, tudo bem?

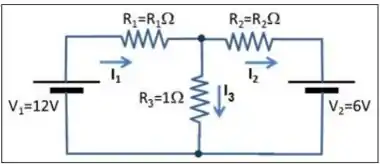
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá? Nas letras (a) e (b) o problema pede para calcularmos as correntes e , que é que passa pela fonte e pelo resistor . Na letra (c) pediu para calcular a potência dissipada pelo resistor . E agora nos pede para calcular a potência dissipara pelo resistor .

Para resolver esse tipo de questão, precisamos aplicar a lei das malhas e a lei dos nós nesse circuito para termos equações suficientes para resolver as correntes.

Resgatando o sistema feito nos itens anteriores, o sistema de equações ficou assim:

I 1 = 3,75 A para a corrente que passa pelo resistor e para a terceira corrente. Agora o problema pede a potência dissipada por . Bom, para isso precisamos lembrar da relação entre potência, resistência e corrente:

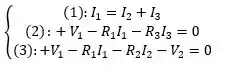
Então precisamos do valor da corrente E calculamos ela no item (b)! Mas antes de sair calculando a potência, vou te relembrar como foram obtidas essas equações!

A primeira equação foi encontrada aplicando a lei dos nós no nó bem de cima do desenho . A segunda foi feita fazendo esse caminho aqui:

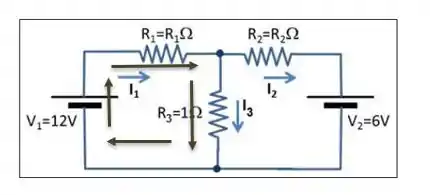
Lembra que quando o caminho está no sentido da corrente (admitida no desenho) a energia do resistor é , e quando a fonte está no sentido positivo é .

A terceira equação foi encontrada aplicando a lei das malhas na malha mais de fora, que passa pelas duas fontes:

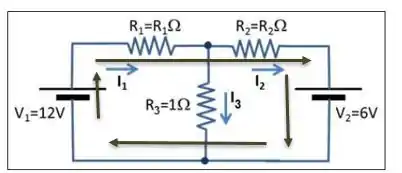
E agora sim podemos calcular a potência dissipada por !