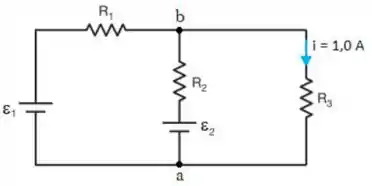
A figura mostra um circuito elétrico onde as fontes de tensões ideais têm fem e . As resistências valem , e . No ramo de a intensidade da corrente é de com o sentido indicado na figura. Sabendo que fem vale e a fem vale , qual é o valor e o sentido da corrente que atravessa o resistor ?
- de para
- de para
- de para
- de para
- de para
Passo 1
Para resolver essa questão, vamos considerar a figura abaixo. Nela, escolhemos a malha no sentido horário e a corrente que passa no resistor no sentido de para .
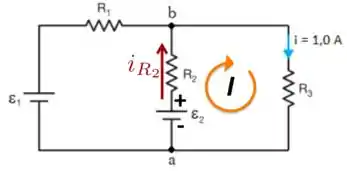
Começando do ponto , vamos utilizar a lei das malhas:
Para você se lembrar, rapidamente, como chegamos na equação acima: porque estamos percorrendo a malha do polo negativo para o positivo da fem; , porque está no sentido da malha e há uma queda de potencial através de ; , porque está no sentido da malha e há um queda de potencial através de
Só somamos todas ddp’s e igualamos a zero, que é a lei das malhas.
Passo 2
Substituindo nessa expressão os valores dados no enunciado, teremos:
Esse sinal de menos que aparece mostra para a gente que escolhemos errado o sentido da corrente , por isso, o sentido correto da corrente em é de para . No entanto, o módulo da corrente continua o mesmo:
Resposta
Letra d.