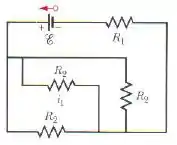
Na figura abaixo e a força eletromotriz da fonte ideal é . Determine
- O valor absoluto de
- O sentido da corrente
Passo 1
- Primeira coisa que a gente faz aqui redesenhar esse circuito pra que ele fique um pouco mais bonitinho. Esse circuito aí é igualzinho a esse aqui. Se liga!
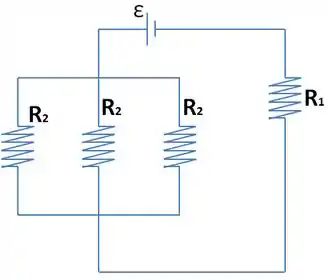
Passo 2
Agora a gente tem que dar aquele chutão pro sentido da corrente. Meu chute é esse aqui!
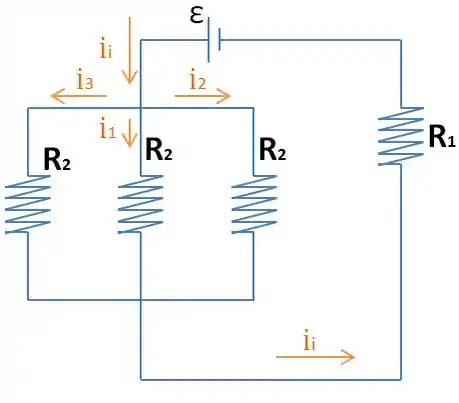
Passo 3
Tem como a gente descobrir logo o valor de ,não tem não?
Só calcular a resistência equivalente aqui que ta bem fácil, já que os três resistores estão em paralelo entre sim, que por sua vez estão em série com .
Passo 4
Agora é só usar a Lei de Ohm.
Passo 5
Presta bem atenção nesse trecho aqui.
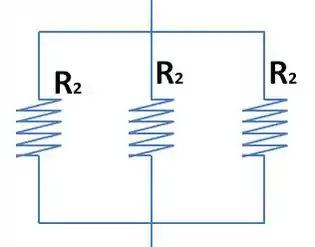
São três resistores iguais, isso significa dizer que as três correntes são iguais. :P
Pela Lei dos nós de Kirchhoff, teremos que:
Mas como são todas iguais
Passo 6
b)
Como a corrente sempre vai da placa de maior para o menor potencial, podemos garantir que o sentido da corrente que eu escolhi está certo, pois lá na fonte a disposição das placas positiva e negativa nos diz isso aí. Mas se houvesse várias fontes aí sim teríamos que usar a Lei das Malhas também.
Poderíamos usar a Lei das Malhas nessa questão, mas aí iria render um sisteminha bem grande e queremos treinar você pra se garantir em todas formas possíveis! :}
Resposta
- Da esquerda pra direita