No circuito da figura abaixo as resistências e e as baterias, consideradas ideais, possuem forças eletromotrizes, e , respectivamente. Determine:
a) O valor absoluto e o sentido (para cima ou para baixo) das correntes , e .
b) A potência dissipada no resistor.
c) A potência fornecida por cada uma das fontes , e .
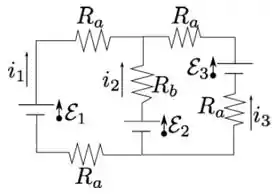
Passo 1
a) O melhor método nesse caso pra calcularmos a corrente, é o método das malhas. Vamos começar nomeando uma corrente para cada uma das duas malhas: e , como mostra a figura abaixo
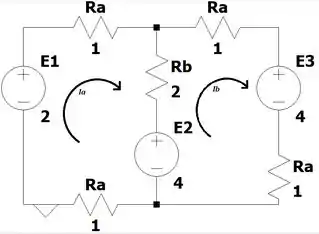
Precisamos aplicar a Lei de Kirchhoff das tensões em cada umas das malhas, para assim chegarmos a um sistema de duas equações e duas incógnitas: e .
Por fim, sabemos que
(tendo como referência a malha direita)
Então, descobrindo e , chegaremos nos valores de , e .
Passo 2
Aplicando a Lei de Kirchhoff das tensões na malha da esquerda:
Agora na malha da direita:
Então, agora temos um sistema com as duas equações que encontramos:
Resolvendo esse sistema, temos que e .
Os sinais negativos de e nos mostram que na verdade, essas correntes estão no sentido contrário ao que definimos na imagem do passo 1, ou seja:
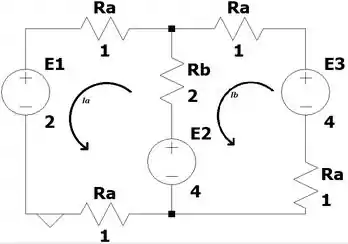
Agora, a partir das relações que a gente estabeleceu no passo 1, podemos encontrar , e
(para baixo, como mostra a figura acima)
Na Lei de Kirchhoff da malha direita, a corrente foi adotada como estando pra cima. Como no cálculo de usamos a malha da direita como referencial e o seu valor deu positivo, concluímos que ela está realmente no sentido que adotamos, ou seja, pra cima.
(para cima)
Passo 3
b) A potência dissipada por um resistor pode ser escrita como
Substituindo o valor de e a sua corrente encontrada no item anterior:
Passo 4
c) A potência fornecida pelas fontes pode ser calculada por
Como a corrente esta contrária ao sentido da fonte, ela esta sendo carregada, absorvendo esta potência e não fornecendo ao sistema.
Resposta
- (para baixo)
(para cima)
(para cima)