No circuito da figura abaixo, temos uma bateria de força eletromotriz (f.e.m) ligada a três resistores de resistências , e e a um capacitor de capacitância que inicialmente (isto é, em ) está descarregado. A chave é fechada em .
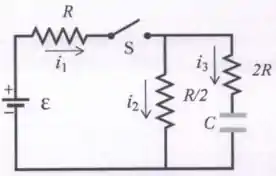
- Calcule os valores das correntes , e logo após o fechamento da chave (ou seja, no instante ).
- Calcule os valores das correntes elétricas , e muito tempo após o fechamento da chave (ou seja, quando ).
Passo 1
a) De acordo com o enunciado, o capacitor começa descarregado, ou seja, em a carga inicial dele é zero. Como a ddp através do capacitor é , então, em .
Apesar de em , a corrente e, como no capacitor, a corrente que passa nele não encontra resistência alguma. A gente pode dizer, por isso, que nesse caso, em , o capacitor é “como um fio sem resistência”: passa uma corrente por ele, mas não há queda de potencial. Resta vermos como ficam as correntes...
Vamos desenhar o circuito como se ele não tivesse o capacitor (já que estamos olhando o instante ), como na figura abaixo.
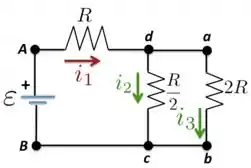
O que temos agora são dois resistores em paralelo, cujo resistência equivalente está em série com o resistor . Vamos encontrar, primeiro, :
Esse resistor equivalente está em série com , de acordo com a figura abaixo.
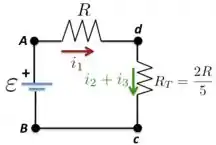
Como está em série com , então a resistência equivalente total será
Passo 2
a) Continuação...
Uma vez que encontramos a resistência equivalente do circuito para , então a corrente total que passa através de nesse instante inicial será dada por
Além disso, sabemos que no nó , temos
Agora, como os resistores e estão em paralelo, eles estão à mesma diferença de potencial , o que permite a gente escrever o seguinte
que, substituindo em , dá
Portanto, temos também que
Passo 3
b) Para um tempo muito grande, ou seja, , o capacitor estará totalmente carregado, porém não passará mais nenhuma corrente por ele, o que significa que a corrente será
Por isso, nesse caso temos os resistores e em série, como está na figura abaixo, e também teremos que .
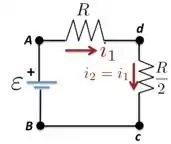
A resistência equivalente nesse instante de tempo será . Portanto, a corrente será